Unifying Two-phase Consensus By A Judgement Model

In the last two blogs, we derived the design of two-phase BFT consensuses. We picked two different routines, namely PBFT and Tendermint. In this blog, we try to unify two-phase consensus by a judgement model.

I. Three Ingredients

Almost all the two-phase consensus consists of three ingredients:

1st-phase vote (1PV)
2nd-phase vote (2PV)
View change process (VC)

1PV corresponds to prepare phase in PBFT or prevote phase in Tendermint; 2PV corresponds to commit phase in PBFT or precommit phase in Tendermint; VC corresponds to view change in PBFT or round change in Tendermint.

II. Necessity of Three Ingredients

It is easy to understand that one-phase vote is necessary for a BFT consensus.

Besides, to rescue the system from a halting status (faluty leader), VC is also necessary.

However, the single-phase vote cannot assure safety across views. To achieve across-view safety, an extra phase of vote is needed. The reason why an extra phase of vote can do it will be presented in the next sections.

Note that the newly-added phase of vote is considered as 1PV in Section I, while the preexisting phase of vote is considered as 2PV in Section I. The reason is that 2PV specifies the time to commit a request, which matches the specification of the preexisting phase of vote.

III. How to Achieve `Safety` Without Compromising `Liveness`?

As already talked about in the PBFT blog, the most challenge task to achieve across-view safety is to judge if an index \(i\) has been committed with a request \(r\) in the old view. Besides, designing the judgement method cannot compromise liveness. Exactly, the judgement result corresponds to the lock primitive in many consensus, such as Tendermint and HotStuff. Based on the judgement, a replica decides if it should vote for a new request or not:

If a replica judges the index \(i\) has been committed with \(r\), it will decline to vote for any other \(r'\) at \(i\) (\(r'\neq r\));
Otherwise, it will vote for any \(r'\).

For a replica to make a judgement, there are mainly two ways:

Make a judgement simply based on its local status.
Collect other replicas' opinions and make a judgement based on the collected opinions;

Next, we talk about how these two ways help make a correct judgement.

IV. Make Judgements Based on Local Status

The judgement based on local status is easy, which can be described as follows:

If a replica possesses a polka for the index \(i\) with \(r\), it would judge \(i\) as committed with \(r\);
Otherwise, it will judge the index \(i\) as uncommitted.

Making judgements basd on local status can guatantee that a committed index \(i\) with request \(r\) will definitely be respected in the new view, thus guaranteeing safety. The reason is that if \(i\) was committed with \(r\), at least \(2/3+\) replicas must possess a polka for it and will not vote for any other \(r'\) at \(i\). Therefore, \(r'\) at \(i\) cannot get \(2/3+\) votes, let alone, be committed.

Next, let us talk about the liveness property. Consider the following two cases：

Case 1: No request is committed at the index \(i\), while some correct replicas possess polka for \(i\) with \(r\);
Case 2: No request is committed at the index \(i\) and no correct replicas possess polka.

For Case 1, once one of the correct replicas possessing polka becomes the leader, it will propose \(r\) for the index \(i\) in the new view. All the correct replicas (with committed or uncommitted judgement results) will vote for \(r\) and \(r\) will finally be committed on each correct replica.

For Case 2, once a correct replica becomes the leader, it can propose an arbitrary \(r'\) for the index \(i\). All the correct replicas will vote for \(r'\) and \(r'\) will also finally be committed on each correct replica. To sum up, liveness can be achieved.

Actually, Tendermint elects this routine.

A. Opmization to achieve `responsiveness`

However, the judgement above may be inefficient. To be more specific, as for Case 1, only when a correct replica possessing polka becomes the leader, will the request be committed. This is also why Tendermint is criticized as being lack of responsiveness.

A direct idea to enhance the responsiveness is to allow the leader to collect the polkas from replicas if there are. This sounds easy, but is hard to achieve. In fact, if a replica possesses a polka for \(r\) at \(i\), the leader only needs to get the value of \(r\) and then proposes \(r\). Therefore, a potential manner is to collect the values of requests at \(i\) from replicas. However, a Byzantine replica can easily fabricate and send an unexisted request \(r'\). And the leader will be stuck in a dilemma, when it receives multiple contradictory requests.

To prevent the Byzantine replicas from sending counterfeit requests, we can add a new phase to the normal case as 0th Phase, shown by the figure below: 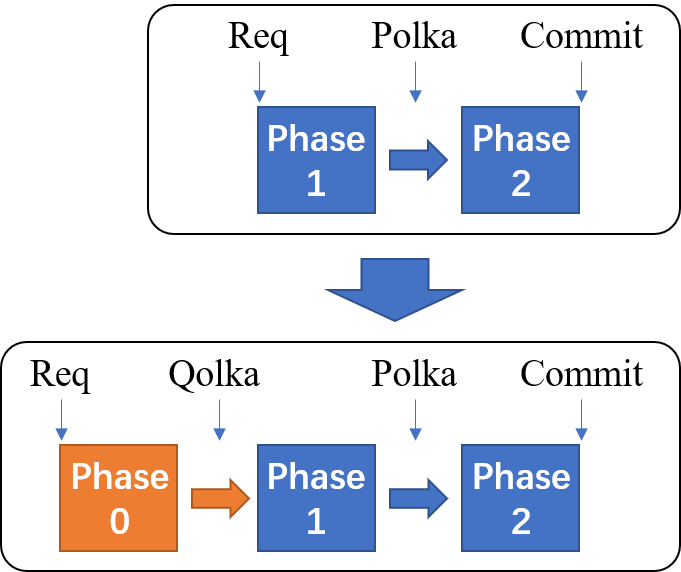An additional phase of phase 0 generates a qolka, which also denotes 2/3+ votes. If a correct replica possesses a polka for \(i\) with \(r\), there must be 2/3+ replicas which possess qolkas. Therefore, the new leader can definitely collect one qolka for \(i\) with \(r\). Besides, since qolka is made up of 2/3+ votes, it cannot be fabricated by Byzanine replicas.

In this regard, if there is a correct replica possessing a polka for \(i\) with \(r\), the new leader can definitely get a consistent qolka and propose \(r\). Therefore, responsiveness is achieved.

Actually, Hotstuff elects this routine: adding a collection of qolka and an extra phase to Tendermint

V. Make Judgements Based on Collected Opinions

A. Formats of opinion expression

The expression of opinions can be of two formats naturally:

Polka/empty (PE for short): a replica broadcasts polka for \(i\) with \(r\) ({polka, \(i\), \(r\)}) if there is one, otherwise empty ({empty, \(i\)});
True/false (TF for short): a replica broadcasts true for \(i\) with \(r\) ({true, \(i\), \(r\)}) if there is a polka, othwewise false ({false, \(i\)});

Note that with PE format, if a replica or multiple replicas collect multiple polkas for an index \(i\), these polkas definitely correspond to the same request r. By contrast, however, with TF format, if a replica or multiple replicas collect multiple true for an index \(i\), these true opinions may correspond to different requests.

B. `PE` format

The PE format is usually assisted with the following judgement rule:

If a replica receives any polka for \(i\) with \(r\), it will judge \(i\) as committed with \(r\) before.
Otherwise, a replica will judge \(i\) as uncommitted before.

The PE format can deduce deterministic, partly-correct, and partly-consistent judgement results in all the correct replicas. To be more specific, when a replica collects 2/3+ opinions for \(i\) with \(r\), we can get the following deduction: \[ C^i(r)=1 \Longrightarrow \forall \space rep_j \space \exists \space polka_r \in O_j^i \] where \(C^i(r)\) denotes whether \(i\) has been committed with a request \(j\), while \(O_j^i\) represents the set of opinions for \(i\) collected by replica \(rep_j\).

Namely, if \(i\) has been committed with \(r\) before, each (correct) replica must collect an opinion of polka on \(i\) with \(r\) and makes the judgement of \(i\) as committed. In this case, all the replicas can make correct and consistent judgements.

By contrast, if \(i\) has not been committed before, some replicas may collect an opinion of polka on \(r\) and makes the judgement as committed, while others may collect all the opinions of empty and make the judgement as uncommitted. In this case, replicas may make inconsistent judgements and some of them may be wrong. We refer to the wrong result (mistaking uncommittedas committed) as False Committed (FC), as an analogy with false positive in machine learning fields.

To sum up, PE format and direct broadcasting of opinions will lead to partly-correct and partly-consistent judgement results.

Partly-correct: Note that FC results (mistaking an uncommitted request as committed) are acceptable, which will not violate the safety property.
Partly-consistent: Inconsistent results are acceptable too. When the replica with committed result becomes the leader, it will repropose \(r\), which will get votes from all the replicas and finally be committed.

Besides, the judgement rule will not lead the system to halt, which guarantees the liveness.

An optimization to `PE`: consistent judgement results

Although the PE format and the assistant judgement rule above are enough to make a correct judgement, it may be inefficient. Particularly, when inconsistent results are gotten by different replicas, the leaders may be switched many times until the replica with committed result becomes the leader.

On the contrary, if all the replicas can get (totally) consistent judgement results, either totally FC or totally correct, the new request proposed by a new leader can be committed soon.

To get the (totally) consistent judgement results, we can carry out an optimization as follows: - Replicas send their opinions to the new sender instead of a broadcast. The new leader packages and broadcasts the collected 2/3+ opinions.

Actually, this optimization is introduced by PBFT, where the opinion is named view change message and the package of opinions is named new view message. From this point, PBFT can be classified as more a three-phase consensus than a two-phase one, since view change is also a phase of message broadcasting.

With this optimization, PBFT can commit new requests at the pace of network delay, thus achieving responsiveness.

C. `TF` format

First of all, the TF format seems to bring lower communication complexity (tiny size of true/false messages) than PE format. However, it also brings some troubles. Following the judgement rules of PE format, the TF format can be assisted with two different judgement rules (rules 1 & 2). However, as we will see below, both rule 1 and rule 2 cannot work well. Therefore, more variants of rules are proposed.

1. Rule 1: based on one `true` （no `safety` or no `liveness`）

The first judgement rule is quite similar to that in PE format:

If a replica receives any true for \(i\) with \(r\), it will judge \(i\) as committed with \(r\);
Otherwise, a replica will judge \(i\) as uncommitted.

A similar deduction can be expressed as follows: \[ C^i(r)=1 \Longrightarrow \forall \space rep_j \space \exists \space true_r \in O_j^i \]

It seems that we can next apply the analysis for PE format in Section V.B to here too. Unfortunately, we cannot! The most essential reason is that an opinion of TF format can be falstified easily. To be more specific, although an committed request \(r\) must correspond to a true in \(O_j\), a Byzantine replica can easily falstify and broadcast an opinion of true for \(r'\). A replica with two true opinions for contradictory requests (\(r\) and \(r'\)) cannot distinguish which one was exactly committed. If a replica elects \(r\) or \(r'\) casually, the system may get a wrong result, thus violating safety. On the contrary, if a replica declines to elect either one, the system may get halted, thus compromising liveness.

By contrast, with the PE format, there would never be two polkas for contradictory requests.

In conclusion, TF format plus rule 1 cannot work well.

2. Rule 2: based on 2/3+ `true` (no `safety`)

The second judgement rule is more conservative:

If a replica receives 2/3+ true for \(i\) with the same request \(r\), it will judge \(i\) as committed with \(r\);
Otherwise, a replica will judge \(i\) as uncommitted.

First of all, different from rule 1, rule 2 can guarantee that:

For each index \(i\), a correct replica will not judge two contradictory requests as committed;
For each index \(i\), if two correct replicas judge \(r\) and \(r′\) as committed respectively, \(r\) must equal \(r′\).

However, collection of 2/3+ true for the same request \(r\) can be non-deterministic, even if \(r\) has been committed before. In other words, a committed request may be mistaken as uncommitted in the new view, which violates safety. In fact, this problem can be named as false uncommitted (FU), which mistakes a committed request as uncommitted. FU is unacceptable.

3. A remedy to rule 2 (Rule 3): Add a new phase

Exactly, we do not need all the correct replicas to judge the committed request (\(r\)) as committed. As long as there are 1/3+ correct replicas do it, there cannot be enough votes for an contradictory request \(r'\), thus guaranteeing safety.

To achieve this, a new phase is added to the normal case, which transforms the two-phase consensus (2PC for short) to a three-phase one (3PC for short), as follows:

1st-phase vote (1PV)
2nd-phase vote (2PV)
3rd-phase vote (3PV)
View change process (VC)

Note that 3PV in 3PC corresponds to 2PV in 2PC, and 1PV in 3PC corresponds to 1PV in 2PC. 2PV in 3PC corresponds to the judgement process. The schematic diagram is shown as below: 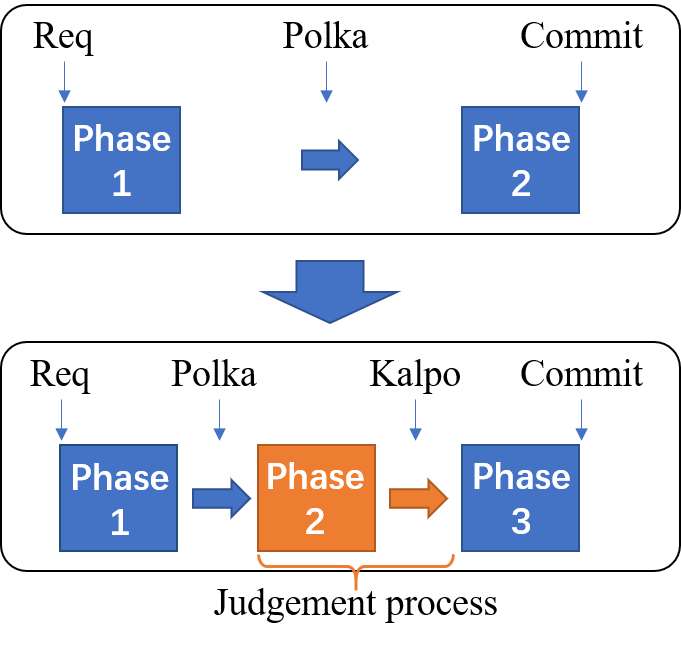The core design of 3PC can be described as folllows:

1PV in 3PC works in the same way as that in 2PC;
In 2PV, a replica will broadcast true opinion if it possesses a polka; otherwise, broadcast false;
If a replica receives 2/3+ true in 2PV, it will broadcast true opinion in 3PV; otherwise, broadcast false;
Only 2/3+ votes are collected in 3PV, will the index \(i\) be committed with \(r\).

For the sake of presentation, we denote the 2/3+ true votes collected in 2PV as kalpo. Therefore, a replica with kalpo will judge \(i\) as committed with \(r\).

Next, we talk about how 3PC achieves safety and liveness respectively.

Safety: If \(i\) is committed with \(r\), at least 1/3+ correct replicas possess a kalpo. These replicas will not vote for an contradictory request \(r'\), thus achieving safety.
Liveness: (1) If no correct replica possesses kalpo, which means each correct replica judges \(i\) as uncommitted, all the correct replicas will vote for a new request \(r'\). Thus, \(r'\) can be finally committed and liveness is achieved. (2) If at least one correct replica possesses kalpo, when it becomes the leader, it will repropose \(r\). \(r\) will be voted by all the correct replicas and be committed. Therefore, liveness can also be achieved.

An optimization to rule 3

As stated in the discussion of liveness above, if one correct replica (\(p\)) possesses kalpo, the system will not go on working, until \(p\) becomes the leader. This can be inefficient.

To accelerate the consensus, an optimization is added to rule 3:

In VC, each replica will broadcast its polka/empty to the new leader;
If the new leader receives a polka for \(r\), it will propose \(r\); otherwise, it can propose an arbitrary request.

As stated before, if any correct replica possesses a kalpo for \(r\), at least 1/3+ correct replicas possess a polka for \(r\). With this optimization, the new leader can definitely receive a polka from the 1/3+ replicas. Therefore, the new leader can definitely propose \(r\), which can get voted by all the correct replicas.

Exacty, Hotstuff can also be considered as electing this routine: TF format + rule 3 + optimization.

4. Rule 4: based on 2/3+ `false` (no `liveness`)

Since collecting 2/3+ true opinions in rule 2 may violate safety, what if we choose the opposite side:

If a replica receives 2/3+ false for \(i\), it will judge \(i\) as uncommitted before.
Otherwise, it will judge \(i\) as committed before.

Besides, since a replica may receive multiple true opinions for inconsistent requests, some of which are sent by Byzantine replicas, we further stipulate that:

The replica receiving true opinions for inconsistent requests will judge \(i\) as undecided. A replica with undecided judgement result will decline to vote for any requests later.

On the other hand, we can get the deduction as follows: \[ C^i(r)=1 \Longrightarrow \forall \space rep_j \space |\{o | o \in O_j^i \& o == false\}|<2/3 \] This deduction plus rule 4 can guarantee safety. The reason is that if \(r\) was committed at \(i\) before, none of replicas can collect 2/3+ false opinions for \(i\). All the correct replicas will judge \(i\) as committed for \(r\) or undecided. Therefore, all these correct replicas will not for a contradictory \(r'\), which guarantee safety.

However, rule 4 cannot guarantee liveness. Consider the example as follows:

No request is committed at index \(i\);
A Byzantine replica arbitrarily broadcasts true opinion for different request \(r_j\) to different replicas \(rep_j\);
\(Rep_j\) judges \(i\) as committed with \(r_j\), and will not vote for any \(r_k\) (\(k \neq j\));
When \(rep_j\) becomes the leader and propose \(r_j\), \(r_j\) cannot get voted by other replicas;
When Byzantine replicas become leaders, they do not broadcast any requests;
The system halts.

5. A remedy to rule 4 (rule 5)

On the basis of rule 4, we can futher stipulate that any replica broadcasting true must also attach polka, in the format of {true, \(i\), \(r\), polka}. In this case, Byzantine replicas cannot send inconsistent requests to different replicas.

In other words, true opinions collected by the correct replicas must correspond to the same request and correct replicas will not judge \(i\) as undecided. Therefore, each correct replica will judge \(i\) as committed or uncommitted. and all the committed requests must be the same. Thus, liveness is achieved.

However, in fact, this remedy leads the format of opinions to be quite like PE format.

Reference

Castro, M., & Liskov, B. "Practical byzantine fault tolerance." In Proceedings of the 3rd USENIX Symposium on Operating Systems Design and Implementation (OSDI'99), pp. 173-186.
Buchman, E. "Tendermint: Byzantine fault tolerance in the age of blockchains." Doctoral dissertation, 2016.
Yin, M., Malkhi, D., Reiter, M. K., Gueta, G. G., & Abraham, I. "HotStuff: BFT consensus with linearity and responsiveness." In Proceedings of the 2019 ACM Symposium on Principles of Distributed Computing (PODC'19), pp. 347-356.

I. Three Ingredients

II. Necessity of Three Ingredients

III. How to Achieve Safety Without Compromising Liveness?

IV. Make Judgements Based on Local Status

A. Opmization to achieve responsiveness