Inspired by the blockchain data structures, lots of streamlined BFT (Byzantine Fault Tolerant) consensus algorithms have been proposed recently, including Tendermint[1], Pili[2], Pala[3], HotStuff[4], and Streamlet[5]. Among them, two extremely-simple ones are quite similar and even born from the same research group (i.e., Prof. Elaine Shi). Streamlet is claimed to be an improved variant of Pala, which seems to be simpler.
In this blog, we try to make a comparison between Pala and Streamlet. Note that we only consider the basic Pala, which takes a democracy-favoring proposer rotation approach, similar to Streamlet. Furthermore, we want to figure out how can Streamlet simplify the consensus and are the improvements made at any costs?
I. A Characteristic Brought by the Consecutive Rule
A. Consecutive rule
Both Pala and Streamlet finalize the notarized blocks based on the consecutive rule, which is defined roughly as follows:
Examples to demonstrate the consecutive rule ofIf two/three adjacent notarized blocks have the consecutive epoch numbers, all the preceding blocks led by the last but one block are considered finailized.
Pala and Streamlet are shown as follows: 
B. Security characteristic brought by two-consecutive-block rule
With the rule of two consecutive blocks, we can deduce a security characteristic that if there are two adjacent notarized blocks with consecutive epoch numbers, there would never be a notarized block with the same height as the former block but with higher epoch number. In other words, we have the deduction as follows: \[ \left. \begin{aligned} N(B_2) = 1 \: \& N(B_1) = 1 \: \& N(B_1') = 1 \\ E(B_2) = E(B_1+1) \\ H(B_2) = H(B_1+1) \: \& H(B_1')=H(B_1) \\ \end{aligned} \ \right \} \Rightarrow E(B_1')<E(B_1) \] where \(N\) denotes if a block is notarized, while \(E\) and \(H\) represent the epoch number and height of a block respectively. This characteristic can also be desmontrated by Figure 2: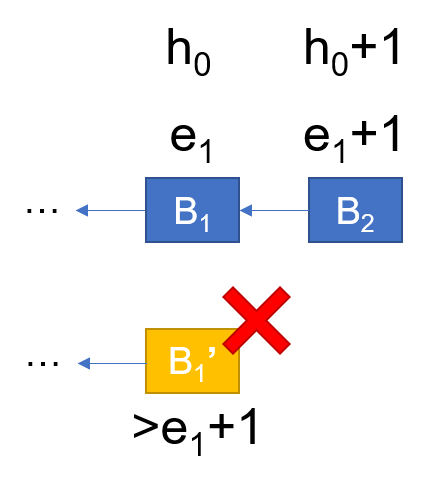
C. Proof of security characteristic
We will prove this security characteristic by contradiction.
Assume that there are two different notarized blocks with the same height and one of them is the former block of two consecutive blocks. As shown by Figure 3, we assume \(B_1\) and \(B_1'\) are different, and \(B_1'\) has a higher epoch number. Simply, we assume \(B_1'\) 's epoch number is \(e_0+3\). Let \(B_0'\) be the preceding block referenced by \(B_1'\).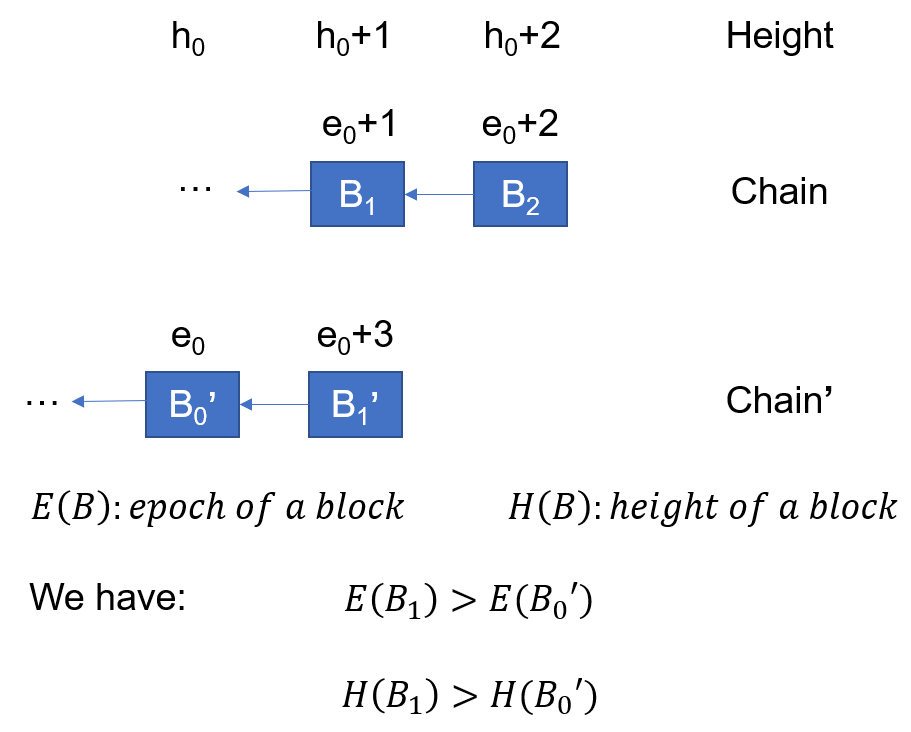
We have that \(E(B_1) > E(B_0')\) and \(H(B_1) > H(B_0')\), where E(B) and H(B) represent the epoch number and height of a block respectively.
On the other hand, both Pala and Streamlet make a similar voting rule that an honest replica will only vote for the block with a higher epoch/height than its local view.
1. Proof for Pala
Pala stipulates the voting rule as follows:
Vote on the proposal iff the following hold: the parent chain led by the proposal is notarized and at least as fresh as the freshest notarized chain the node has observed.
In short, a replica in Pala will vote for a block, only if the block extends from its local notarized chain and the block's precursor's epoch number is higher than or equal to the largest-epoch notarized chain.
Back to the above figure in Section I.C, for an honest replica with chain as its local notarized chain, there must be at least \(f+1\) honest replicas possessing the notarized chain up to block \(B_1\).
On one hand, if \(B_0'\) is not a prefix of \(B1\), all these \(f+1\) honest replicas will not vote for \(B_1'\), since \(B_1'\) does not extend their local notarized chain.
On the other hand, if \(B_0'\) is a prefix of \(B1\) (shown by the following figure), all these \(f+1\) honest replicas will not vote for \(B_1'\) as well, since \(B_0'\)'s epoch number is lower than \(B_1\).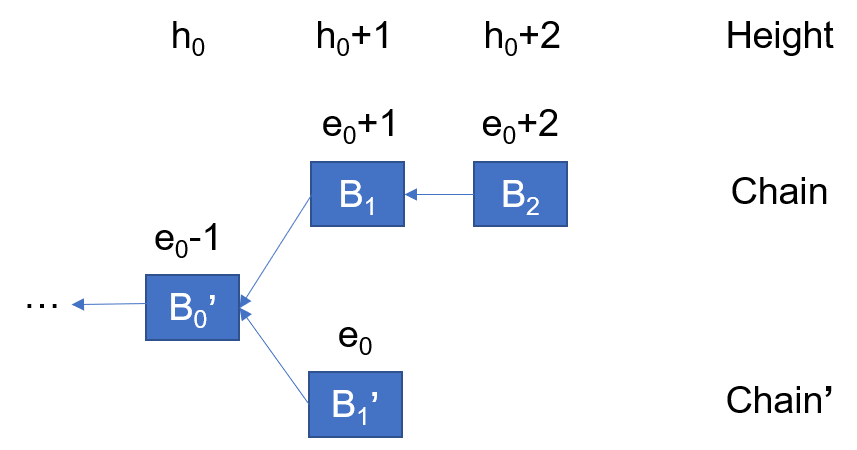
Pala
Therefore, \(B_1'\) cannot receive \(2f+1\) votes or notarized. We reach a contradiction.
2. Proof for Streamlet
Streamlet stipulates the voting rule as follows:
Every player votes for the first proposal they see from the epoch's leader, as long as the proposed block extends from (one of ) the longest notarized chain(s) that the voter has seen.
In short, a replica in Streamlet will vote for a block, only if the block extends from its local notarized chain and the block's precursor's height is higher than or equal to the longest notarized chain.
Back to the above figure in Section I.C, for an honest replica with chain as its local notarized chain, there must be at least \(f+1\) honest replicas possessing the notarized chain up to block \(B_1\). Since \(B_0'\)'s height is lower than \(B_1\), all these \(f+1\) honest replicas will not vote for \(B_1'\).
We reach a contradiction too.
II. Supplement to the Security Charateristic
From Section I, we can conclude that if there are two adjacent notarized blocks with consecutive epoch numbers, and there is another notarized block with the same height as the former block, the block's epoch must be lower than the former block., which is shown by Figure 5: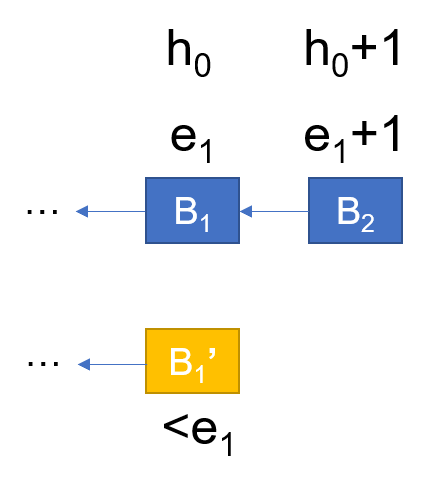
A natural thought is that can we add some supplementary rules to the two-consecutive-block rule, to make \(B1'\) with a lower epoch number impossible to be finalized?
Towards achieving this, Pala and Streamlet chooses different routines. In short, Pala remakes use of the voting rule described above, which is based on the definition of fresher than relationship. By contrast, Streamlet strengthens the consecutive-block rule from two to three.
Next, we talk about how these two routines can be a supplementary to the two-consecutive-block rule.
A. Routine of Pala
Note that in Pala, a notazied block with a lower epoch number can exist, as examplified by Figure 6, where both \(B_1\) and \(B_1'\) can be notarized. 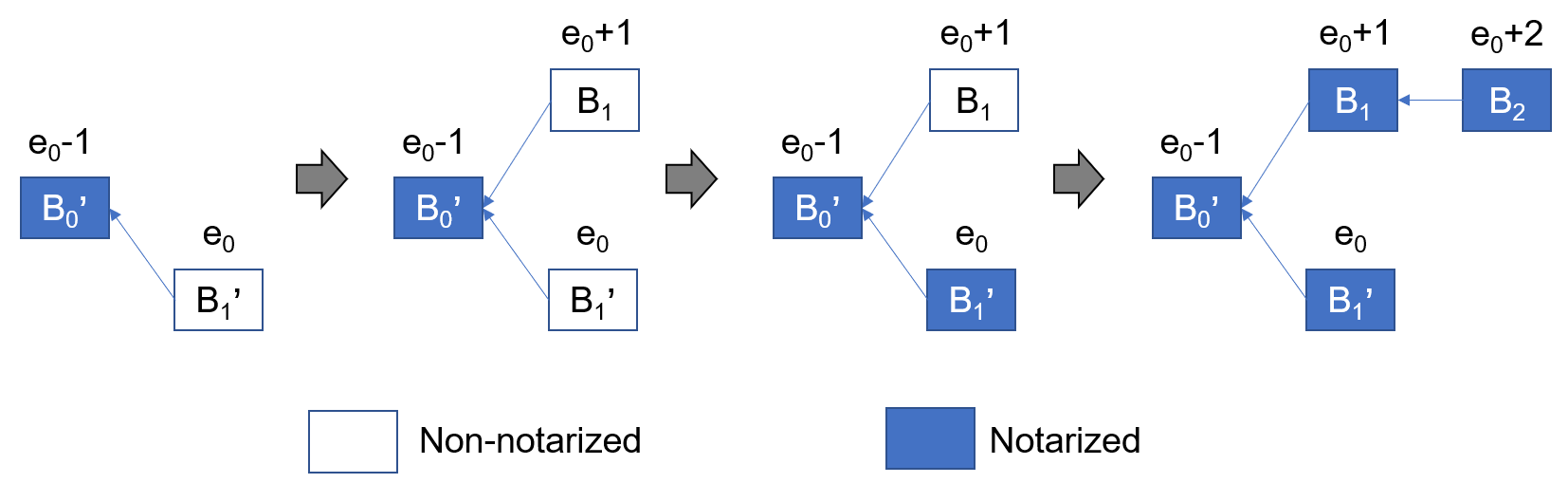
Pala
Pala can guarantee that \(B_1'\) will never be referenced by a later notarized block, as Figure 7 shows: 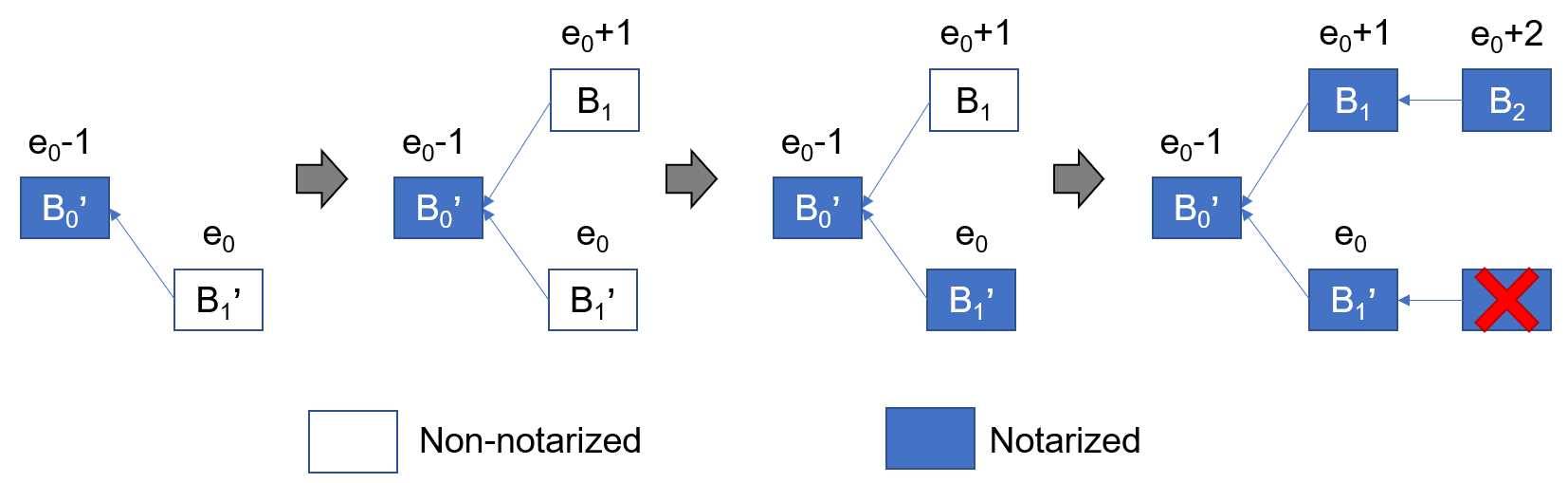
Pala
1. Proof for Pala
The reason why \(B_1'\) will never be referenced by a later notarized block can be described as follows. We describe the reason by contradiction. We simply assume that the later block is \(B_2'\), whose epoch number is \(e_0+3\): 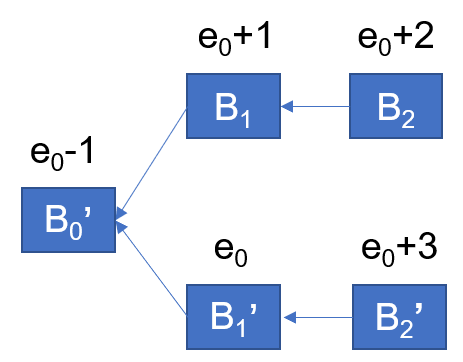
Pala
However, since \(B_2\) is notarized, at least \(f+1\) honest replicas must have voted for \(B_2\) and possess the notarized block \(B_1\). These replicas will not vote for \(B_2'\), since its precursor block \(B_1'\) has a lower epoch number than \(B_1\). Therefore, \(B_2'\) cannot get more than \(2f+1\) votes or be notarized, thus reaching a contradiction.
To sum up, there will be no successor notarized block after \(B_1'\). If we stipulate that a block can be finalized by the two-consecutive-block rule, there will be no contradictory finalized blocks. This is exactly stipulated by Pala.
B. Routine of Streamlet
On the contrary to Pala, with the voting rule in Streamlet, \(B_1'\) can also be referenced by a later notarized block, examplified by Figure 9: 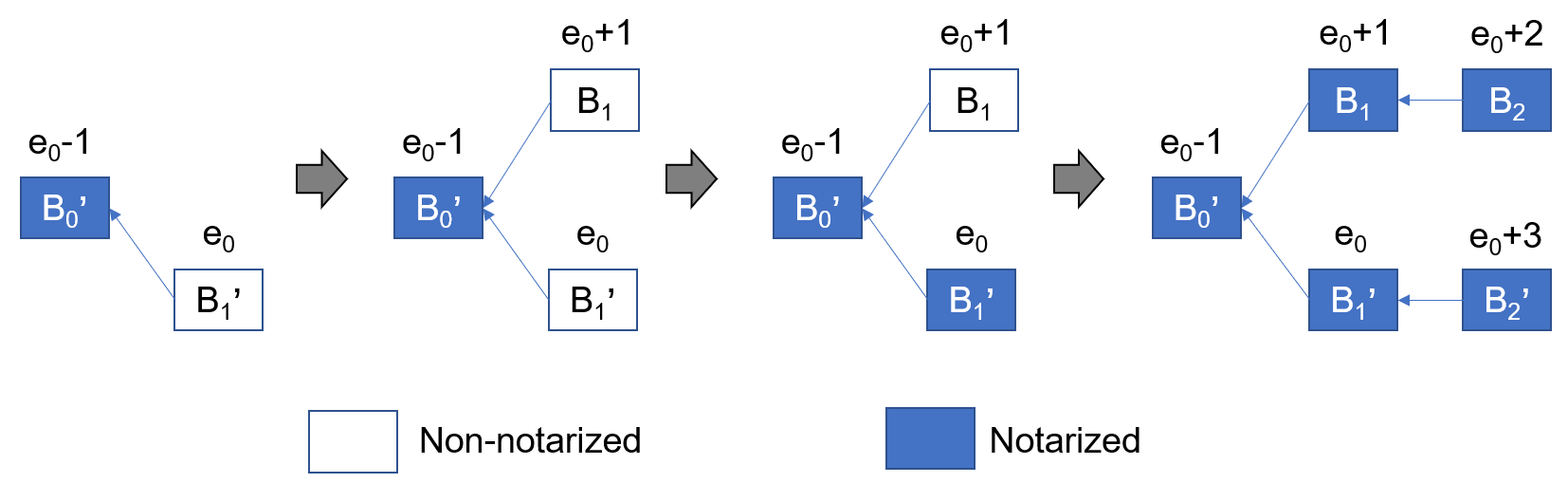
Streamlet
To be more specific, all the blocks \(B_1\), \(B_2\), \(B_1'\), and \(B_2'\) can be notarized.
To guarantee safety,Streamlet picks another routine, which strengthens the finazliation rule from two consecutive blocks to three consecutive blocks. Under the three-consecutive-block rule, we have that if there are three adjacent notarized blocks with consecutive epoch numbers, there will not be another notarized block with the same height as the middle block, examplified as follows: 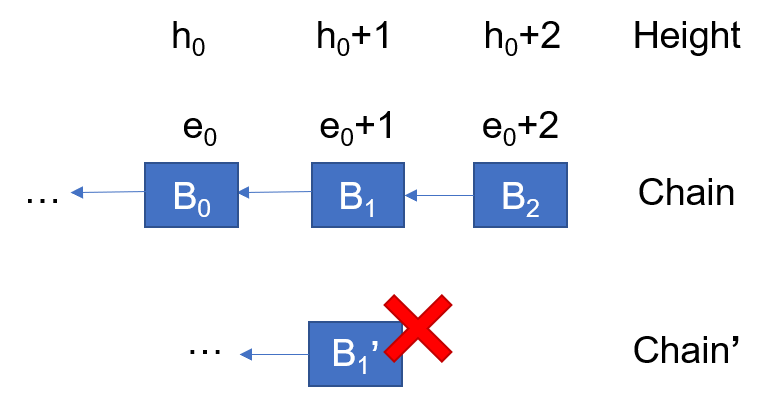
Streamlet
1. Proof for Streamlet
Next, we explain why the three-consecutive-block rule in Streamlet can guarantee that there will not be another notarized block with the same height as the middle block, thus achieving safety.
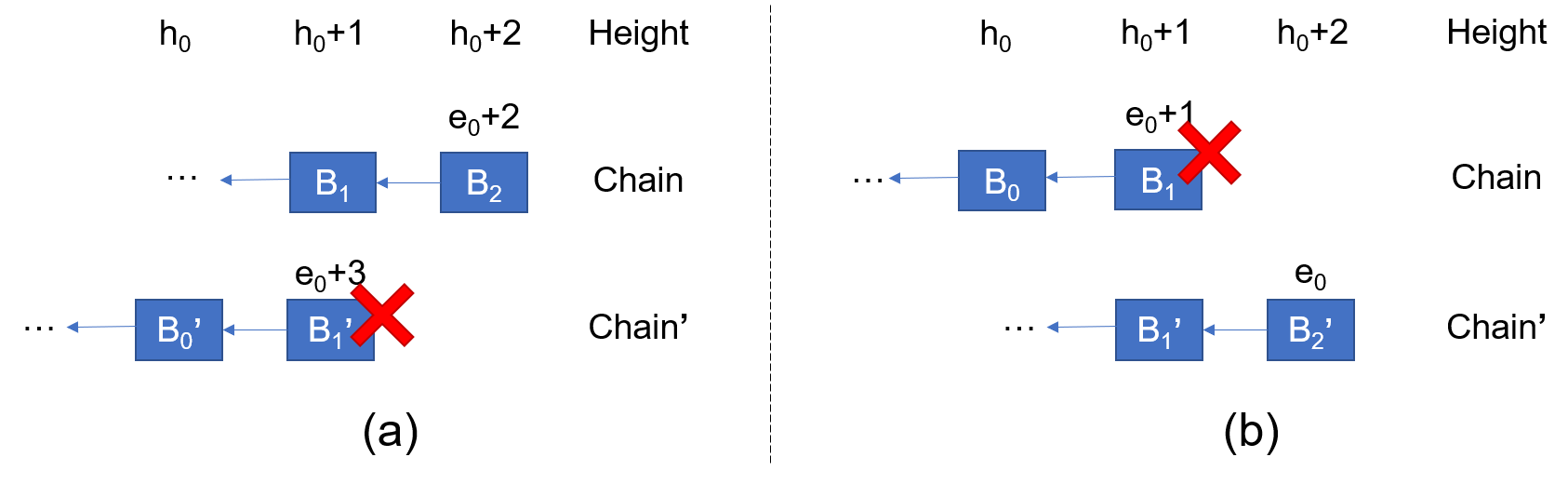
Streamlet
Combining Figure 11(a) and Figure 11(b), we can get the proof for Streamlet. We describe it in two cases, with the Figure 12 as an example.
- Case 1 shown by Figure 12(a): \(B_1'\) cannot have an epoch number larger than \(e_0+2\), which can be directly deduced from Figure 11(a).
- Case 2 shown by Figure(b): we prove it by contradiction. Assume that \(B_1'\) has an epoch number lower than \(e_0\), for example \(e_0-1\). According to Figure 11(b), \(B_0\) cannot be notarized, which is contradictory to the existence of three-consecutive-blocks (\(B_0\), \(B_1\), and \(B_2\)). Therefore, \(B_1'\) cannot have an epoch number lower than \(e_0\)
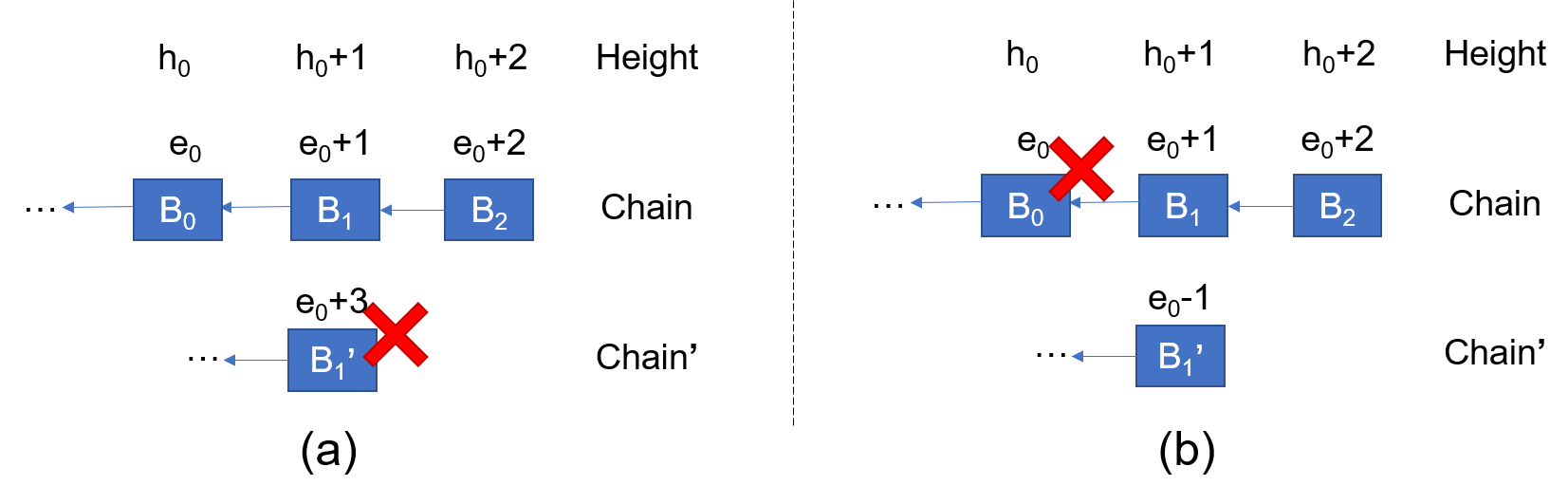
Streamlet
III. Conclusion
Pala has a simpler finalization rule but a more complicated voting rule than Streamlet, as shown by Table 1. In general, specification of Pala is a little more complex than Streamlet, since its introduction of fresher than relation. However, two-consecutive-block finalization rule can be easier to attain, which makes Pala more efficient.
Table 1. A simple comparison
| Rule | Pala |
Streamlet |
|---|---|---|
| Voting rule | Fresher than relation (epoch based) | Height based |
| Finalization rule | Two consecutive blocks | Three consecutive blocks |
A. A simple comparison of two adjacent blocks between Pala and Streamlet
If we only consider two adjacent blocks, different cases can be demonstrated by Figure 13, where the number in Figure 13 represents the epoch number. 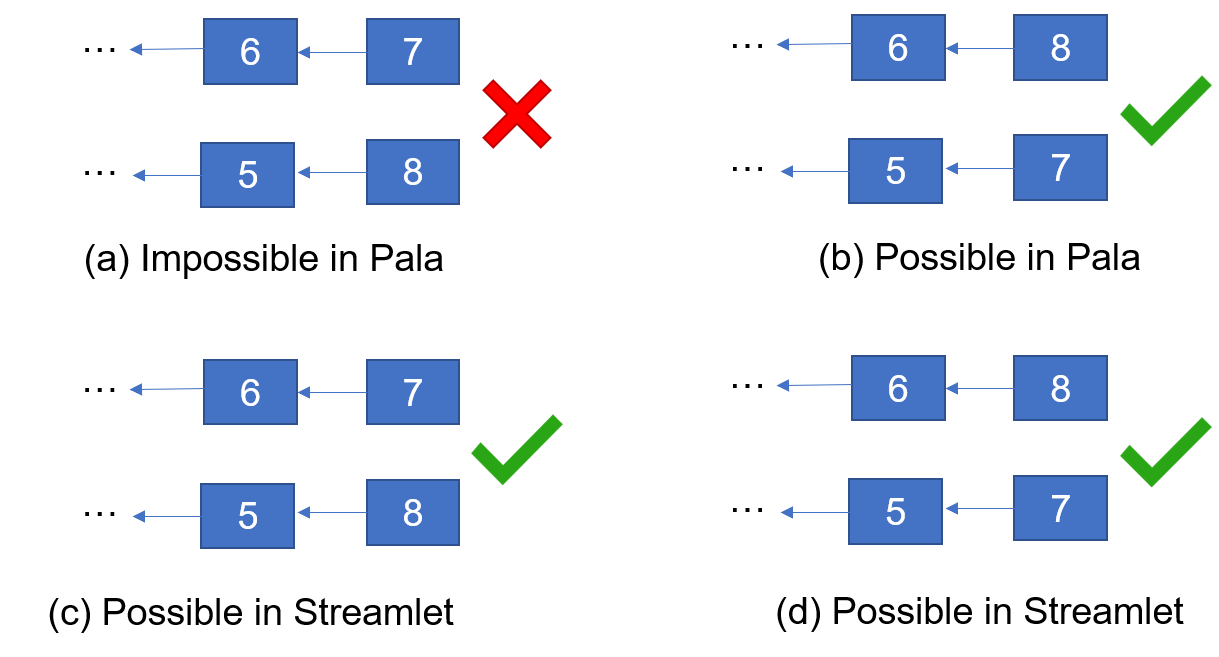
As can be seen from Figure 13, cases of (b) and (d) are possible, which indicates the two-block (non-consecutive) rule is not enough for Streamlet or Pala. Case of Figure 13(c) shows that even the two-consecutive-block rule is not enough for Streamlet. However, the two-consecutive-block rule is enough for Pala, as shown by Figure 13(a).
Reference
- Buchman, E. "Tendermint: Byzantine fault tolerance in the age of blockchains." Doctoral dissertation, 2016.
- Chan, T. H., Pass, R., & Shi, E. "PiLi: An Extremely Simple Synchronous Blockchain." Cryptology ePrint Archive, 2018.
- Chan, T. H., Pass, R., & Shi, E. "Pala: A simple partially synchronous blockchain." Cryptology ePrint Archive, 2018.
- Yin, M., Malkhi, D., Reiter, M. K., Gueta, G. G., & Abraham, I. "HotStuff: BFT consensus with linearity and responsiveness." In Proceedings of the 2019 ACM Symposium on Principles of Distributed Computing (PODC'19), pp. 347-356.
- Chan, B. Y., & Shi, E. "Streamlet: Textbook streamlined blockchains." In Proceedings of the 2nd ACM Conference on Advances in Financial Technologies (AFT'20), pp. 1-11.