Understanding the Safety of Chained HotStuff

As for the chained HotStuff, there are two commitment rules for a block: three-chain or two-chain+QC. Three-chain rule is easy for understanding, while two-chain+QC is not.

In this blog, we want to figure out why the commitement rule can be relaxed from a three-chain to a two-chain+QC? Or in other words, why a two-chain+QC can guarantee the safety, where three-chain can be considered as a special case of two-chain+QC?

I. Commitment rule: Three-chain or Two-chain+QC

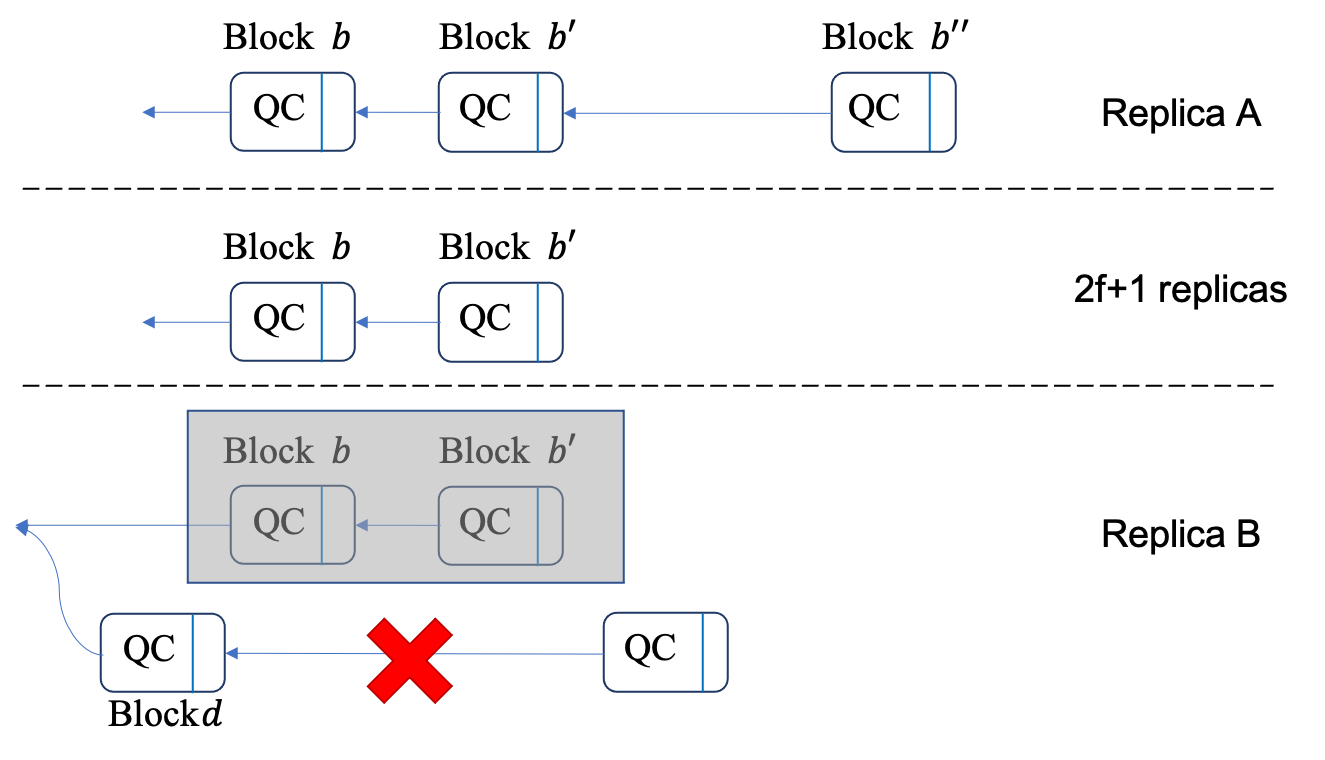
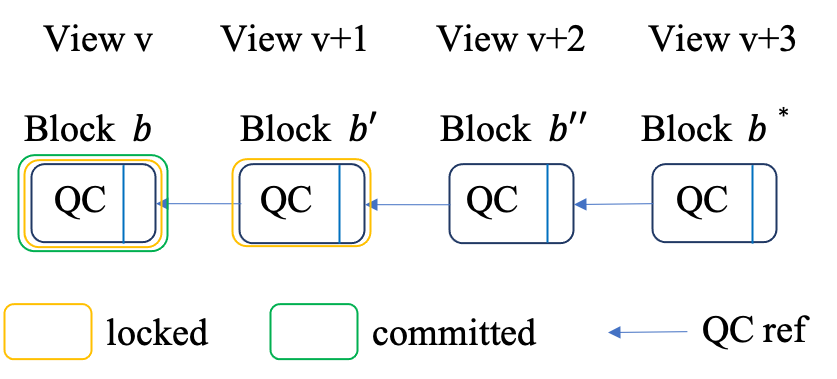
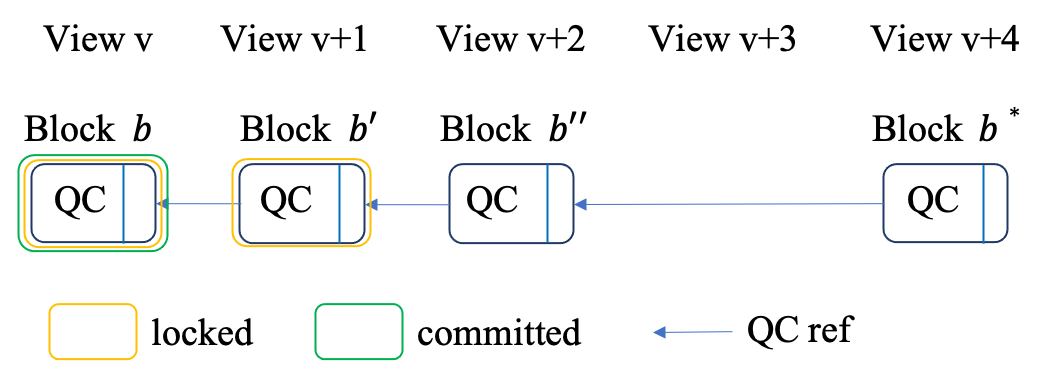
In the HotStuff paper, a block ($b$) is allowed to be committed if the blocks following $b$ form a three-chain, shown as Figure 1: Figure 1. Three-chain rule In fact, the commitment requirement can be relaxed to under a two-chain and a general QC, as Figure 2 shows: Figure 2. Two-chain+QC rule

In the figure, Blocks $b$, $b'$, and $b''$ form a two-chain, and Block $b^*$ contains a general QC to reference $b''$.

This relaxed commitment requirement can be found in both the HotStuff paper and the author's presentation slides. To be more specific, in Algorithm 4 of the HotStuff paper, lines 10-11 only check the two-chain rule and line 5 shows the general QC from $b^*$ to $b''$. Related pseudocodes are transcribed as follows: Figure 3. Pseudocodes in HotStuff paper The 23-rd and 24-th slides of hotstuff-podc-slides also take an example to show this relaxed requirement. For the convenience of readers, we copy these two slides as follows directly: Figure 4(a). Page 23 in HotStuff slides Figure 4(b). Page 24 in HotStuff slides

II. How can two-chain+QC ensure safety?

We prove the safety in two ways: one is to draw an anology to Pala, and the other is to prove the safety directly.

A. Proof by an analogy to Pala

We argue that HotStuff is quite similar to Pala, whose voting rules are based on epoch. The distinction though is that HotStuff includes QC in the block, particularly in the descendant block. Therefore, we have the following analogies:

• a general QC involving two blocks in HotStuff resembles the one certified block in Pala, shown by Figure 5(a).
• an one-chain plus a general QC in HotStuff resemble the two consecutive certified blocks in Pala, shown by Figure 5(b).
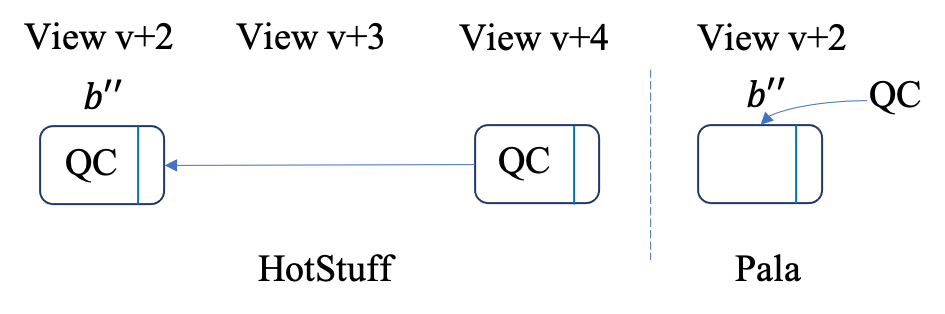
• a two-chain plus a general QC in HotStuff resemble the three consecutive certified blocks in Pala, shown by Figure 5(c).

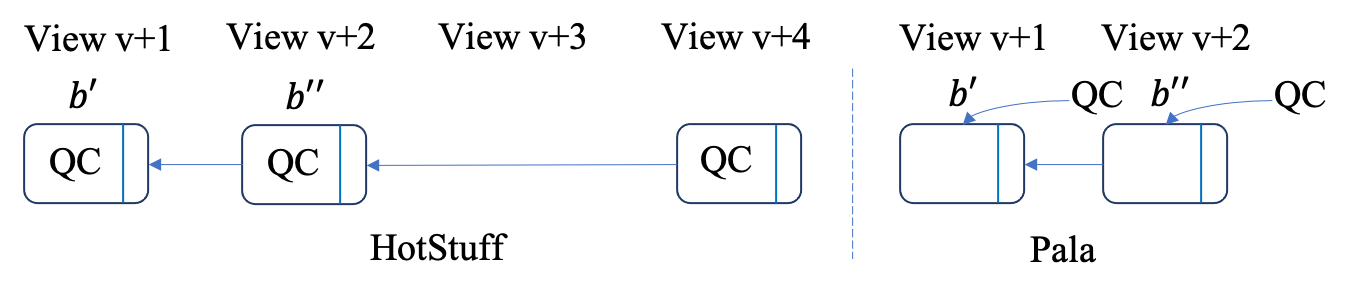
Figure 5(a). General QC in HotStuff resembles certified block in Pala Figure 5(b). One-chain+QC in HotStuff resembles two consecutive certified block in Pala Figure 5(c). Two-chain+QC in HotStuff resembles three consecutive certified block in Pala

Since we have proved Pala's safety with two-consecutive-notarized blocks in a previous blog, we can easily conclude that an one-chain+QC in HotStuff is enough to guarantee the safety.

In fact, HotStuff proposes a stronger requirement, namely two-chain+QC, which can definitely ensure the safety too.

B. Proof by analysing HotStuff directly

An analogy to Pala may not be intuitive enough. Therefore, we do an analysis on HotStuff directly in this section.

1. Lemma 1

First, we put forward a lemma (Lemma 1) as follows:

If a block $b$ is referenced by a two-chain, any block $d$ referenced by a generic QC is either an ancestor or a descendant of $b$.

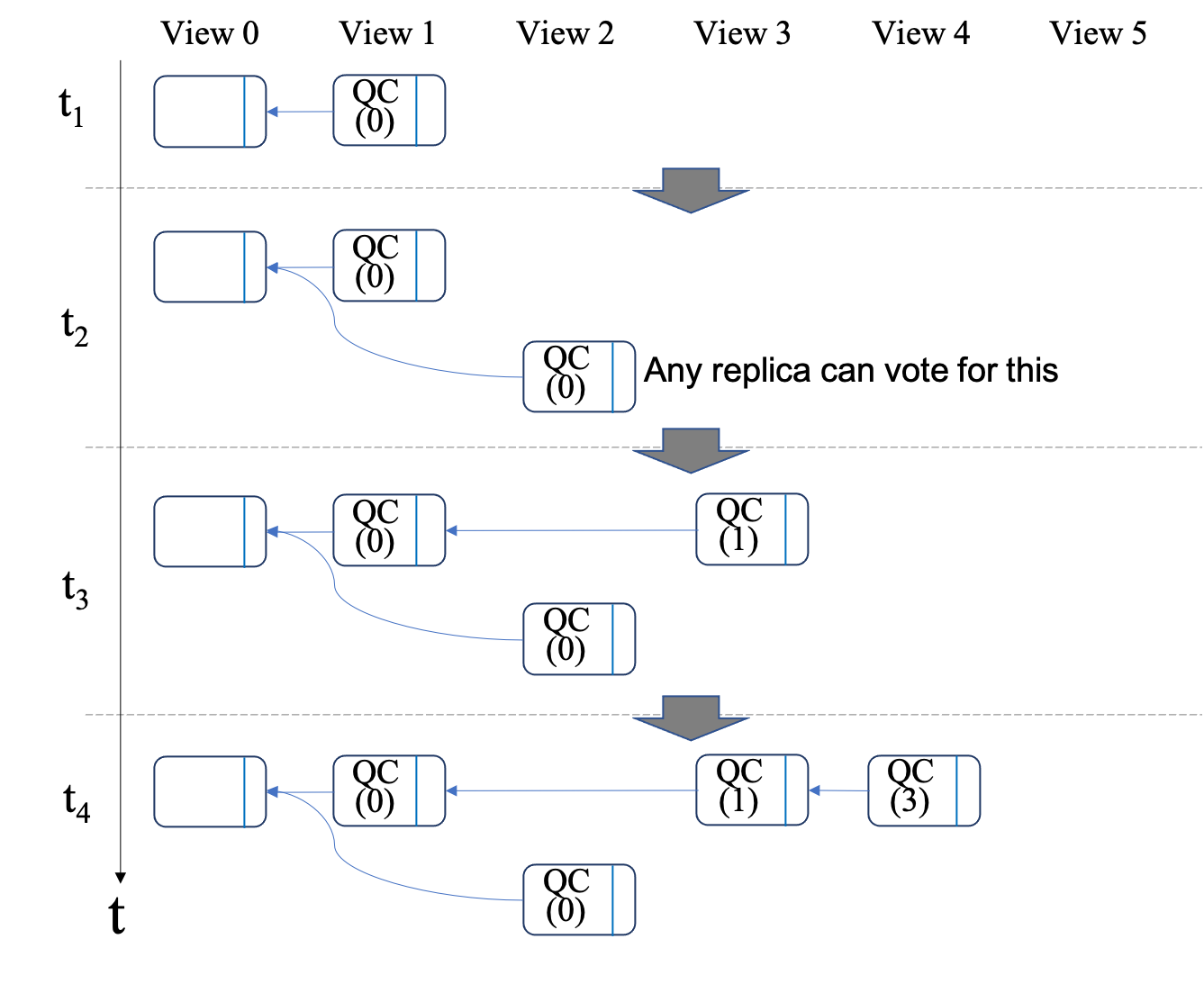
Proof for the lemma is as follows. Consider an example in Figure 6. Assume in replica $A$, block $b$ is referenced by a two-chain. Therefore, at least $2f+1$ replicas will possess an one-chain referencing $b$. For a block $d$ in replica $B$, which is contradictory to $b$, it will not get votes from the above $2f+1$ replicas. The reason is that, QC in $d$ has the same view number as $b$. Therefore, a replica voting for $b$ will not vote for $d$ and $d$ will not get $2f+1$ votes. In other words, all the blocks referenced by a generic QC must be an ancestor or a descendant of $b$. Figure 6. Lemma 1

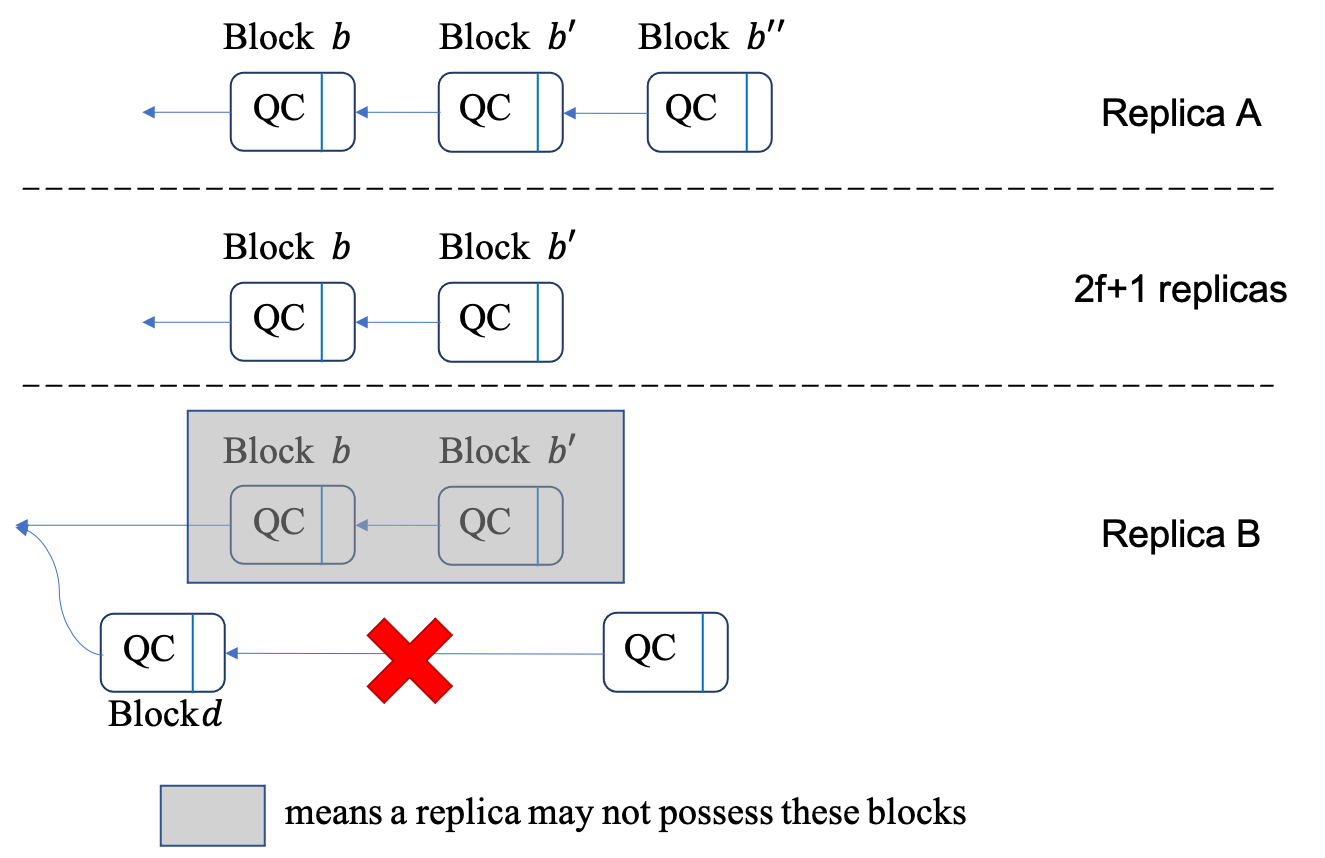
2. Proof by an example

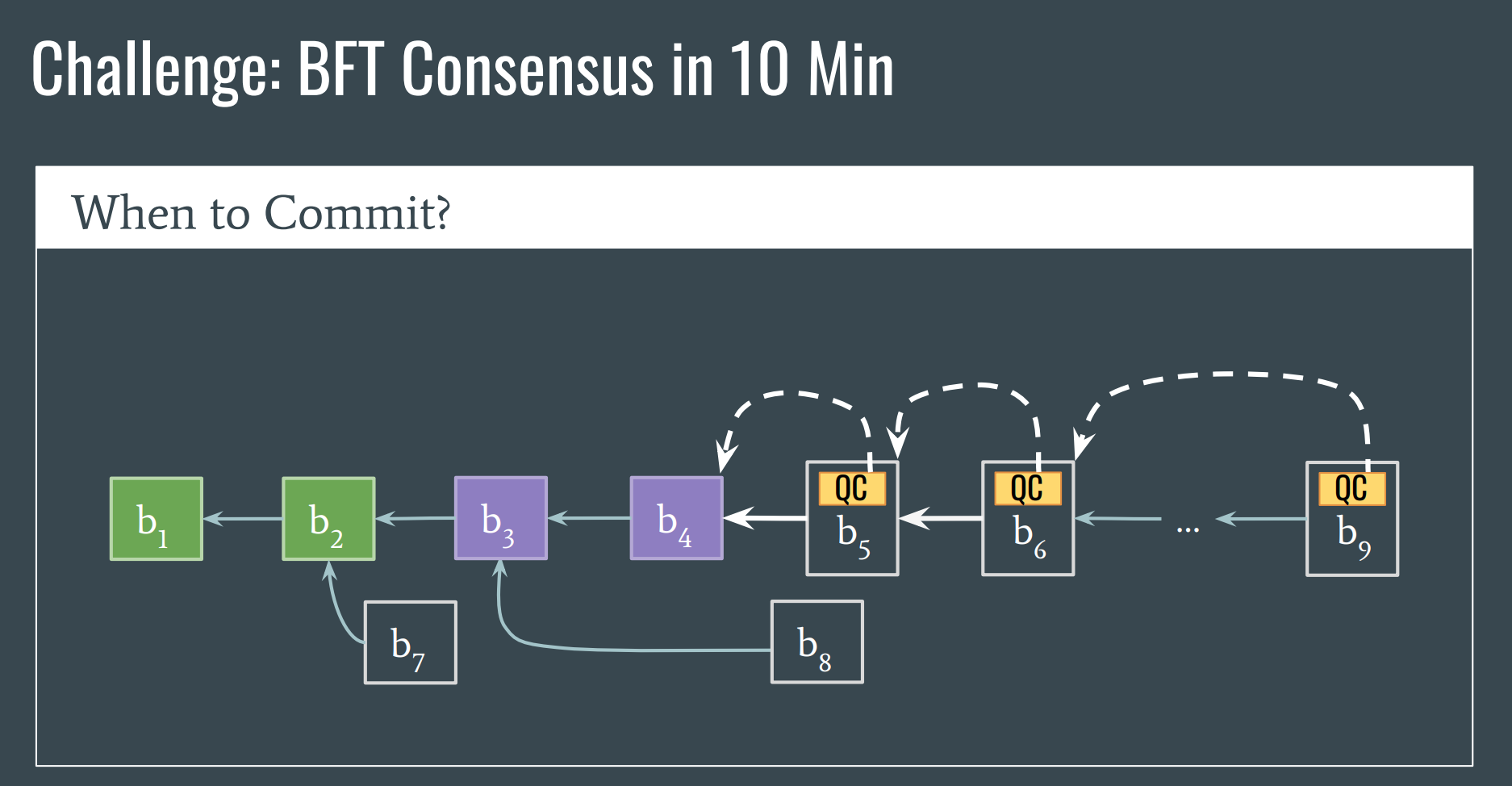
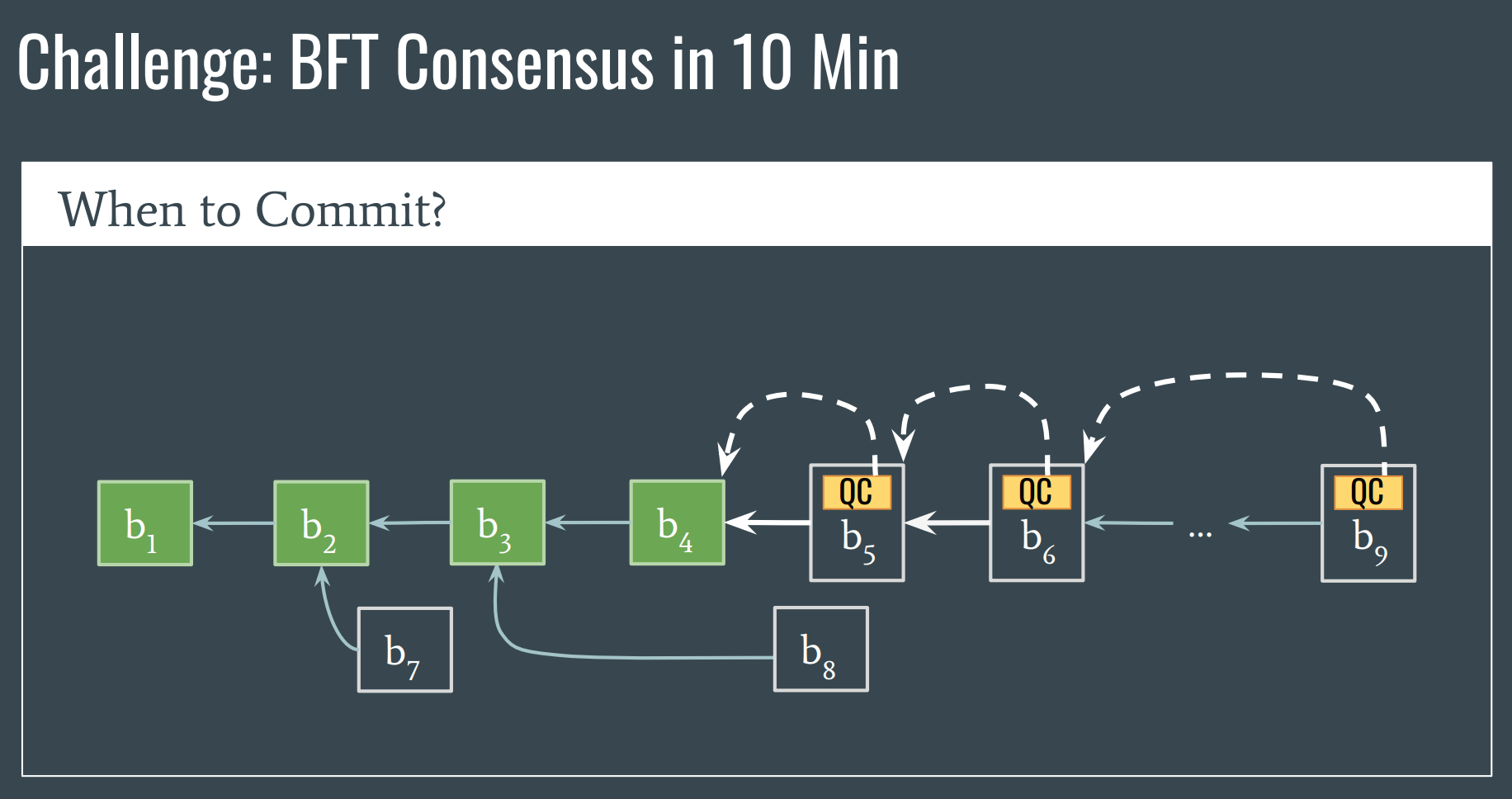
We will not prove the safety by a rigorous theoretical analysis, which will be boring and intuitive. By contrast, we prove it by an example in following figure.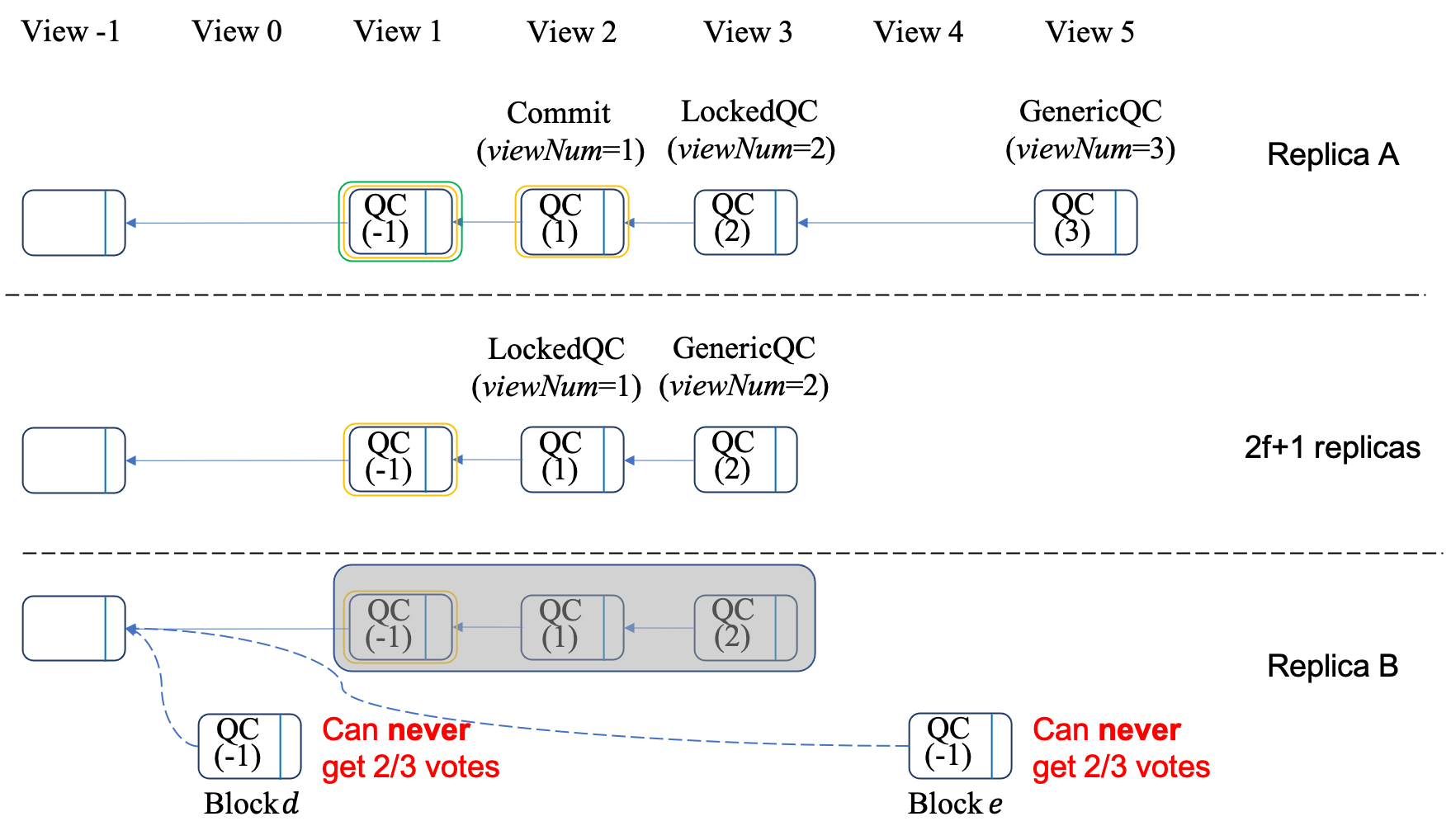 Figure 7. Proof of two-chain+QC

In the example, we consider a scenario: if a block is committed by the two-chain+QC rule in a replica ($A$), will a contradictory block ($d$ or $e$) get a QC in other replicas ($B$)?

The answer is no, which can be deduced by lemma 1 directly.

III. Why QC+two-chain cannot ensure safety?

We explain the reason by an example in Figure 8. 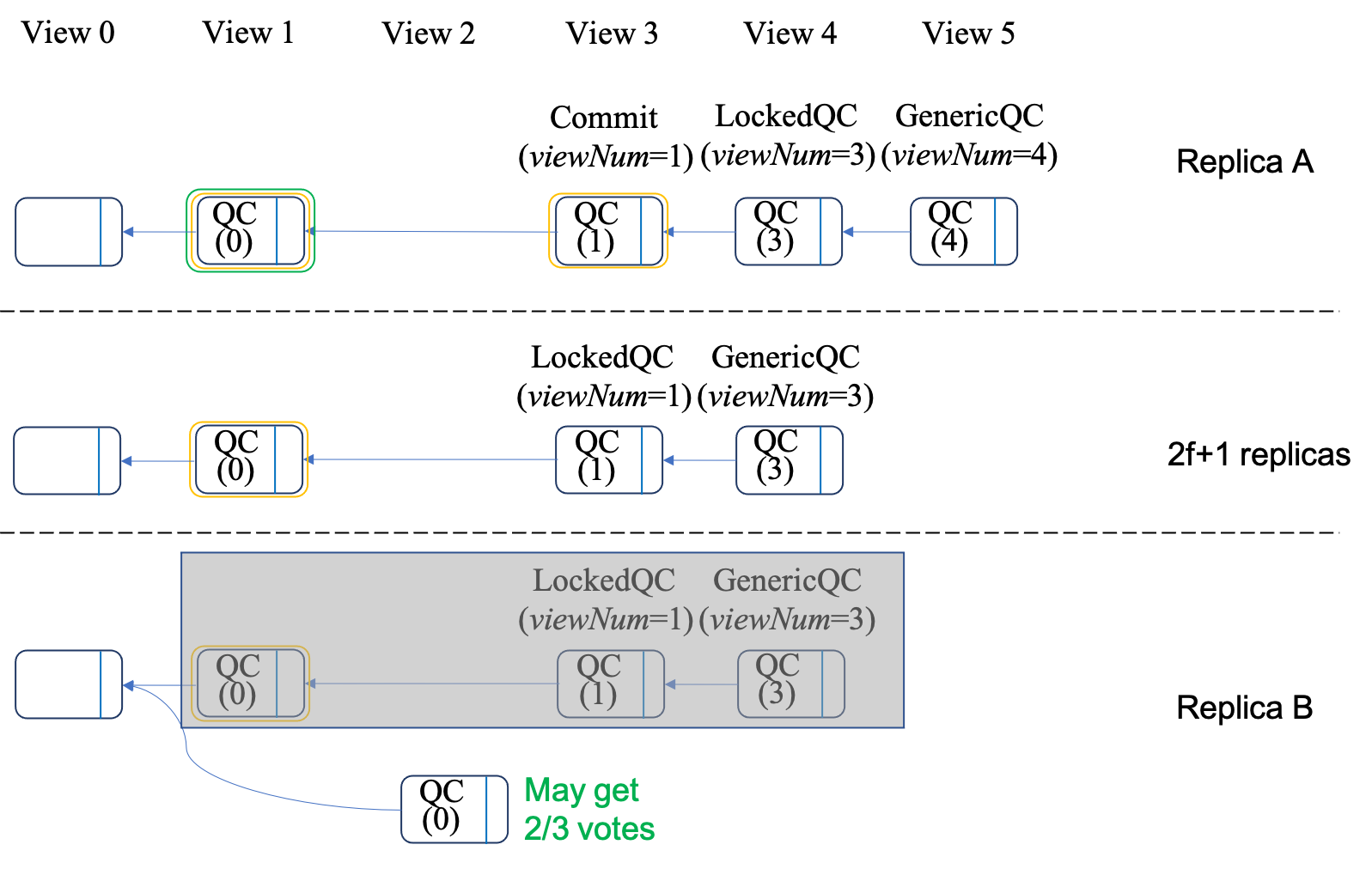Figure 8. Example of QC+two-chain

In Figure 8, a replica $A$ commits a block by a QC+two-chain. Therefore, at least $2f+1$ replicas can lock the block by a QC+one-chain. However, we argue that a contradictory block in replica $B$ can get $2f+1$ votes too.

Next, we show how to construct the viewpoint in replica $B$ in the following figure. Figure 9. Viewpoint from replica B

Therefore, even if a block is committed in a replica, there may be another contradictory block being committed in other replicas.

IV. Why one-chain+QC+one-chain can ensure safety?

Exactly, a variant commitment rule one-chain+QC+one-chain can also ensure the safety. The proof is quite similar to the two-chain+QC.

A. Proof by an analogy to Pala

As explained before, one-chain+QC in Hotstuff is actually identical to the two-consecutive blocks in Pala, which can guarantee the safety.

B. Proof by analysing HotStuff directly

1. Lemma 2

We put forward Lemma 2 as follows, whose schematic diagram is shown by Figure 10:

If a block $b$ is referenced by a one-chain+QC, any block $d$ referenced by a generic QC is either an ancestor or a descendant of $b$.

Figure 10. Lemma 2

The proof is also similar to Lemma 1, which is omitted here.

2. Proof by an example

The safety can be proved easily with Lemma 2. We simply show the proof by an example in the following figure.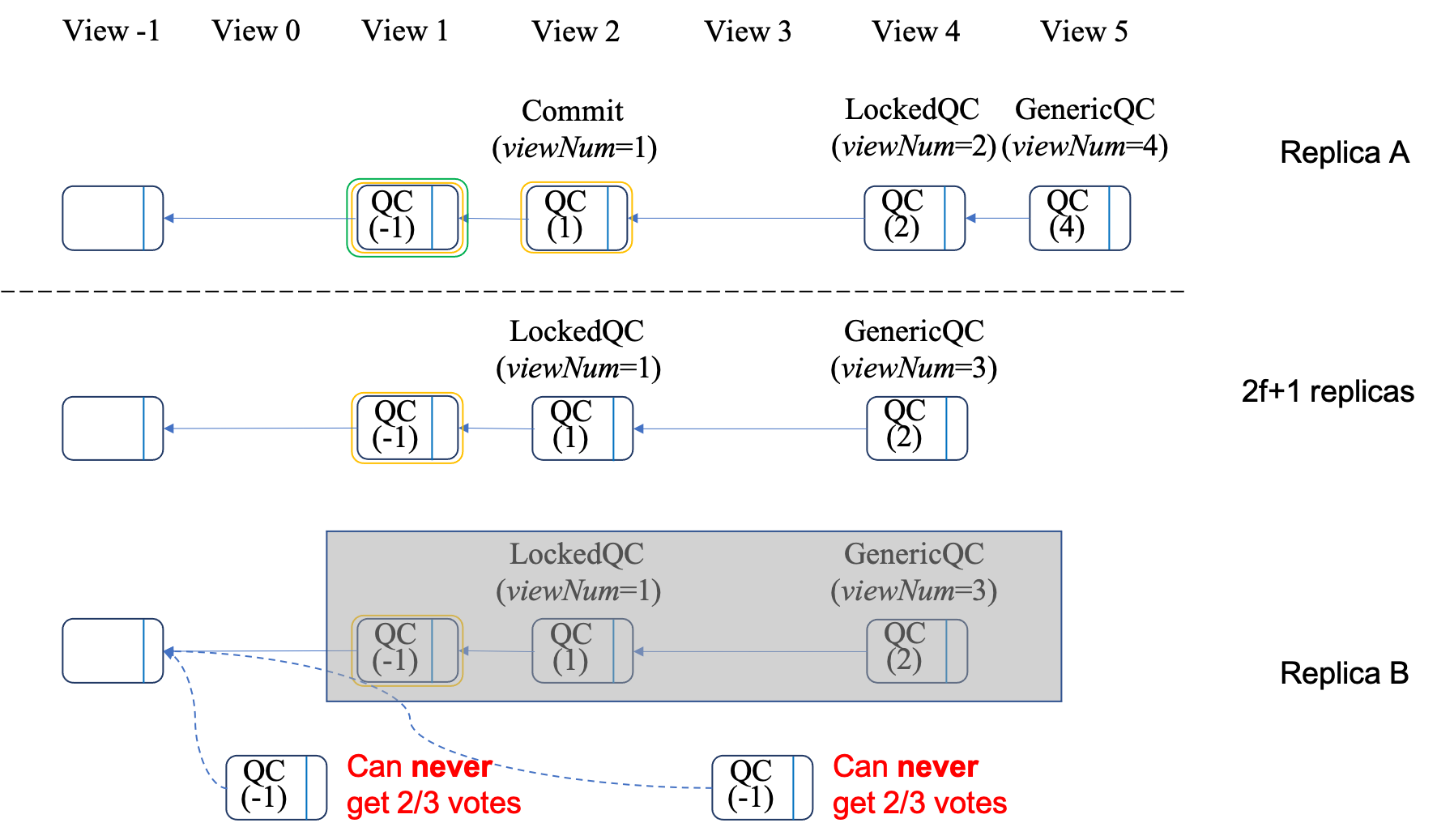 Figure 11. Example of one-chain+QC+one-chain

V. Safety of Two-phase HotStuff

Exactly, a two-phase HotStuff can guartantee the safety, which is presented at the end of the HotStuff paper. The proof for its safety is also easy, since one-chain+QC in Hotstuff is actually identical to the two-consecutive blocks in Pala.

The reason why three-phase is needed is that it further provides the responsiveness property. The analysis on the responsiveness is made in the next blog.

Reference

1. Chan, T. H., Pass, R., & Shi, E. "Pala: A simple partially synchronous blockchain." Cryptology ePrint Archive, 2018.
2. Yin, M., Malkhi, D., Reiter, M. K., Gueta, G. G., & Abraham, I. "HotStuff: BFT consensus with linearity and responsiveness." In Proceedings of the 2019 ACM Symposium on Principles of Distributed Computing (PODC'19), pp. 347-356.
3. hotstuff-podc-slides