In the classical paper The Byzantine Generals Problem, Lamport et al. proposed two recursive protocols to achieve the Byzantine consensus, namely oral message protocol and signed message protocol. Although the authors have proved the correctness of the protocols, the proof seems to be not intuitive enough.
In this blog, we try to prove the oral message protocol by myself. Particularly, I will attach the figures to make the proof more readable.
1. Symbols Description
\(S\): the set of all the replicas {\(p_1\), \(p_2\), ..., \(p_m\)}
\(H\): the set of all the honest replicas
\(F(n, f, S)\): \(f\) Byzantine replicas in \(n\) replicas
\(F(n, S)\): \(F(n, f)\) where the number of Byzantine replicas is implicit
\(F^{L \in H}(n, f, S)\): \(F(n, f, S)\) where the leader is honest.
\(M(y^1, y^2, ..., y^r)\): a function which outputs the value of the majority
\(M_i\): \(M(y^1, y^2, ..., y^r)\) run by the replica \(p_i\)
2. Oral Message Protocol
2.1 Protocol Definition
\(F^{L=p_l, r}(n, S)\) = \(M(y^{1, r-1}, y^{2, r-1}, ..., y^{n-1, r-1})\), where: \[ y^{k,r} = \begin{cases} F^{L=p_k, r}(n-1, S|p_l), & r \geq 1 \\ x_{p_l ->p_k}, & r=0 \end{cases} .............(1) \] and \(x_{p_l ->p_k}\) represents the message sent from \(p_l\) to \(p_k\). For a system with up to \(f\) Byzantine replicas, each replica runs the protocol with initial \(r\) as \(f\), namely \(F^{r=f}\).
2.2 Theorem 1
For a system consisted of \(n\) replicas, wherein at most \(f\) replicas are Byzantine, if \(n \geq\) 3\(f\)+1 and each honest replica runs the oral message protocol, then \(\forall p_i, p_j \in H\): \(F_i\) = \(F_j\). Furthermore, if the leader \(L\) is honest and broadcasts \(m\), \(\forall p_i \in H\): \(F_i^{L,r}\) = \(m\).
In other words, Theorem 1 argues that the oral message protocol can achieve the consensus.
3. Proof of Message Protocol
We first propose and prove two lemmas, i.e., Lemma 1 and Lemma 2. Based on these two lemmas, we finally prove Theorem 1.
3.1 Lemma 1
3.1.1 Description of Lemma 1
If \(n \geq 2f+2\) and \(F_i^{L \in H, r}(n-1, f)\) = \(F_j^{L \in H, r}(n-1, f)\), then \(F_i^{L \in H, r+1}(n,f)\) = \(F_j^{L \in H, r+1}(n, f)\).
3.1.2 Proof of Lemma 1
Let \(y_i^{k, r}\) denote the value of \(y^{k,r}\) figured out by the replica \(p_i\).
According to the assumption that \(F_i^{L \in H, r}(n-1, f)\) = \(F_j^{L \in H, r}(n-1, f)\), for a cluster of \(n-1\) replicas, if the leader \(p_k \in H\), then: \[ \forall p_i, p_j \in H, y_i^{k, r}=y_j^{k, r} .............(2) \]
Therefore, for a cluster \(S\) of \(n\) replicas, if the leader \(p_l \in H\) and broadcasts the message \(m\), \(\forall p_k \in H\), \(p_k\) receives \(m\) and will broadcast \(m\) in the sub-round of \(F^{L=p_k, r}(n-1, f, S|p_k)\).
In the sub-round of \(F^{L=p_k, r}(n-1, f, S|p_l)\), according to Equation (2), \(\forall p_i, p_j \in H\), \(y_i^{k, r}\)=\(y_j^{k, r}\)=\(m\).
In other words, for a replica \(p_a\), if \(p_k \in H\), the input argument \(y_k\) for the function \(M_a\) will be the same as \(m\). Since \(n \geq 2f+2\), the majority of the input arguments for \(M_a\) will be the same as \(m\). Therefore, \(F_i^{L \in H, r+1}(n, f)\) = \(F_j^{L \in H, r+1}(n, f)\).
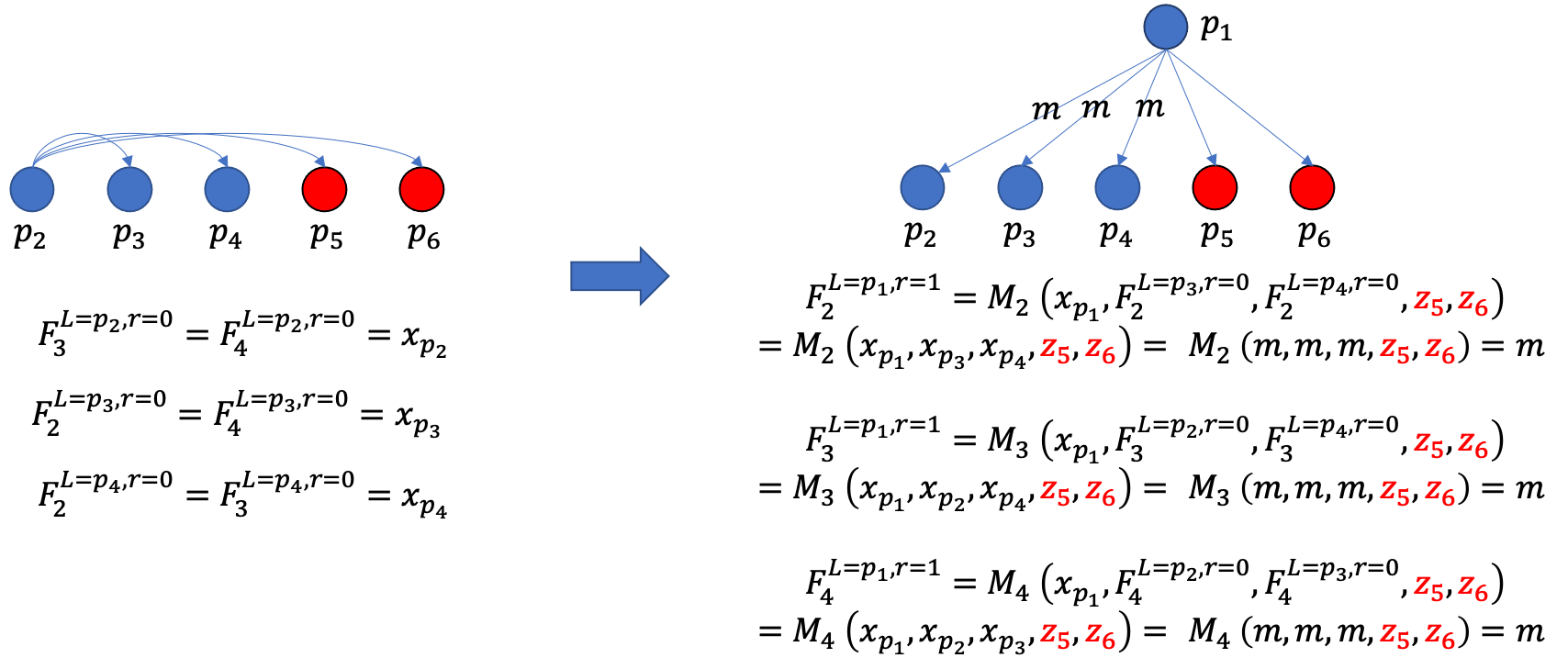
3.1.3 A simple example to demonstrate Lemma 1
We demonstrate the proof by a simple example, as shown by Figure 1. Figure 1. shows the Lemma 1 when there are six replicas with two Byzantine ones. Particularly, the leader is honest. We consider the situation where \(r\)=0.
In the left figure, the honest replicas will accept the messages from the leader directly, according to the \(r\)=0 case in Equation(1). Namely, \(F_k^{L=p_j,r=0}\)=\(x_{p_j}\), where \(x_{p_j}\) denotes the messages sent from \(p_j\).
In the right figure, the honest leader \(p_1\) broadcasts \(m\). Each honest replica (\(p_2\), \(p_3\), and \(p_4\)) will also broadcast \(m\) in the sub-round of \(F\). Therefore, the arguments for the function \(M\) will contain three messages of \(m\) and decide \(m\) as the result.
3.2 Lemma 2
3.2.1 Description of Lemma 2
If \(n \geq\) 3\(f\) and \(f \geq\) 2, \(\forall p_i, p_j \in H\), \(F_i^{L \in H, r=f-1}(n, f)\)=\(F_j^{L \in H, r=f-1}(n, f)\)
3.2.2 Proof of Lemma 2
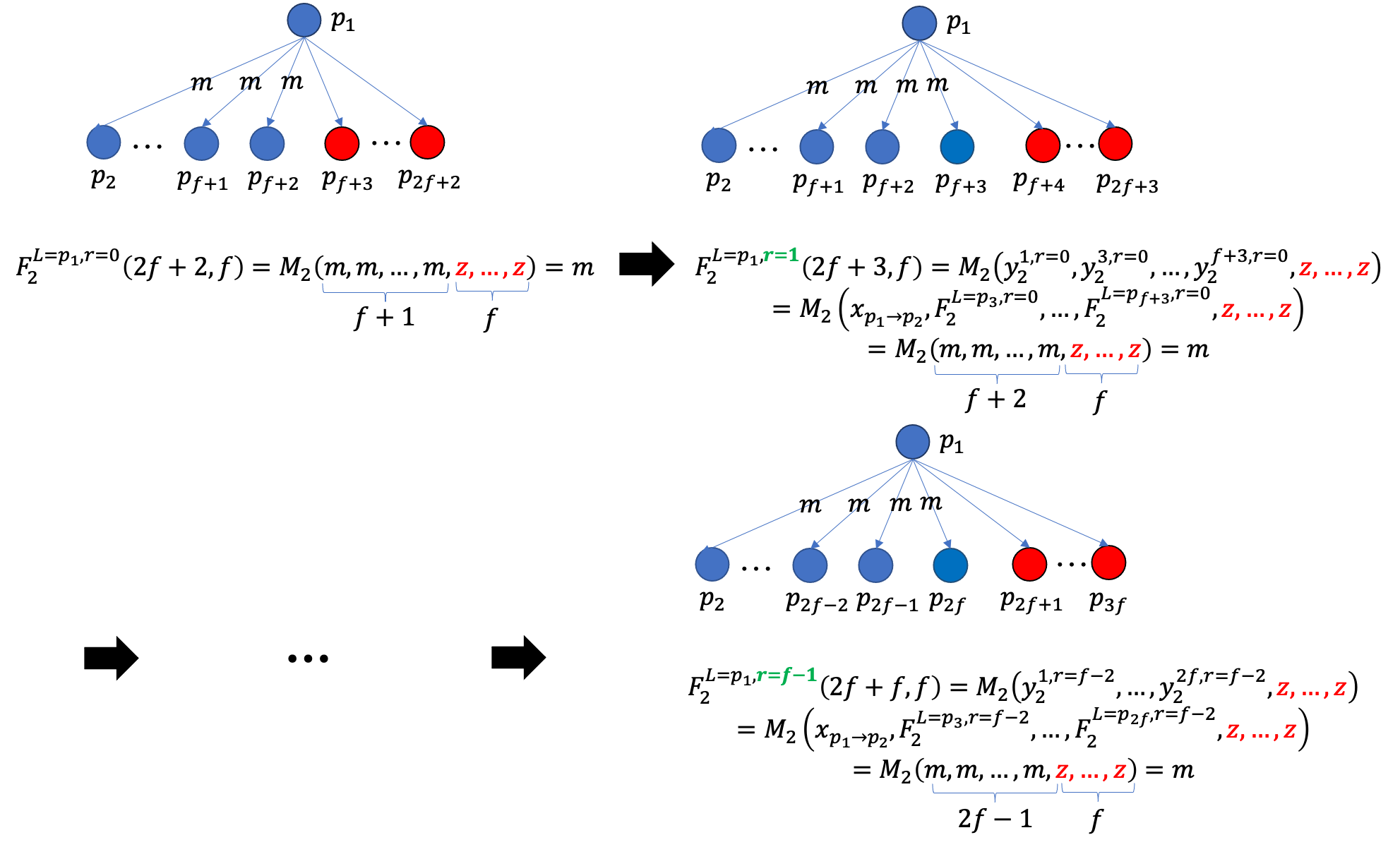
When the round \(r\) is 0, \(y^{k, r=0}\)=\(F^{L \in H, r=0}\) = \(x_{p_l ->p_k}\).
Therefore, \(F^{L \in H, r=1}(2f+2, f)\) = \(M(y^{1, r=0},y^{2, r=0}, ..., y^{2f+1, r=0} )\)=\(M(x_{p_l ->p_1}, x_{p_l ->p_2}, ..., x_{p_l ->p_{2f+1}})\). Since the replica set {\(p_1, p_2, ..., p_{2f+1}\)} contains \(f\)+1 honest replicas, the value set {\(x_{p_l ->p_1}, x_{p_l ->p_2}, ..., x_{p_l ->p_{2f+1}}\)} contains at least \(f\)+1 same message \(x\) broadcast by \(p_l\). Thus, \(F_i^{L \in H, r=1}(2f+2,f)\)=\(F_j^{L \in H, r=1}(2f+2,f)\)=\(x\).
According to Lemma 1, we have \(F_i^{L \in H, r=2}(2f+3,f)\)=\(F_j^{L \in H, r=2}(2f+3,f)\).
By analogy, we have \(F_i^{L \in H, r=f-1}(2f+f,f)\)=\(F_j^{L \in H, r=f-1}(2f+f,f)\). Namely, for \(n\)=3\(f\), \(F_i^{L \in H, r=f-1}(n,f)\)=\(F_j^{L \in H, r=f-1}(n,f)\).
Furthermore, we have \(\forall n \geq\) 3\(f\), \(F_i^{L \in H, r=f-1}(n,f)\)=\(F_j^{L \in H, r=f-1}(n,f)\)
3.2.3 A figure to depict the proof of Lemma 2
3.3 Proof of Theorem 1
We will prove it via the mathematical induction.
- When \(f\)=1 and \(n\)=4, it is easy to prove the correctness of Theorem 1.
- Assume that for \(f\) and \(n \geq\) 3\(f\)+1, Theorem 1 is correct. Namely, \(\forall p_i, p_j\), \(F_i^{r=f}(n, f)\) = \(F_j^{r=f}(n, f)\).
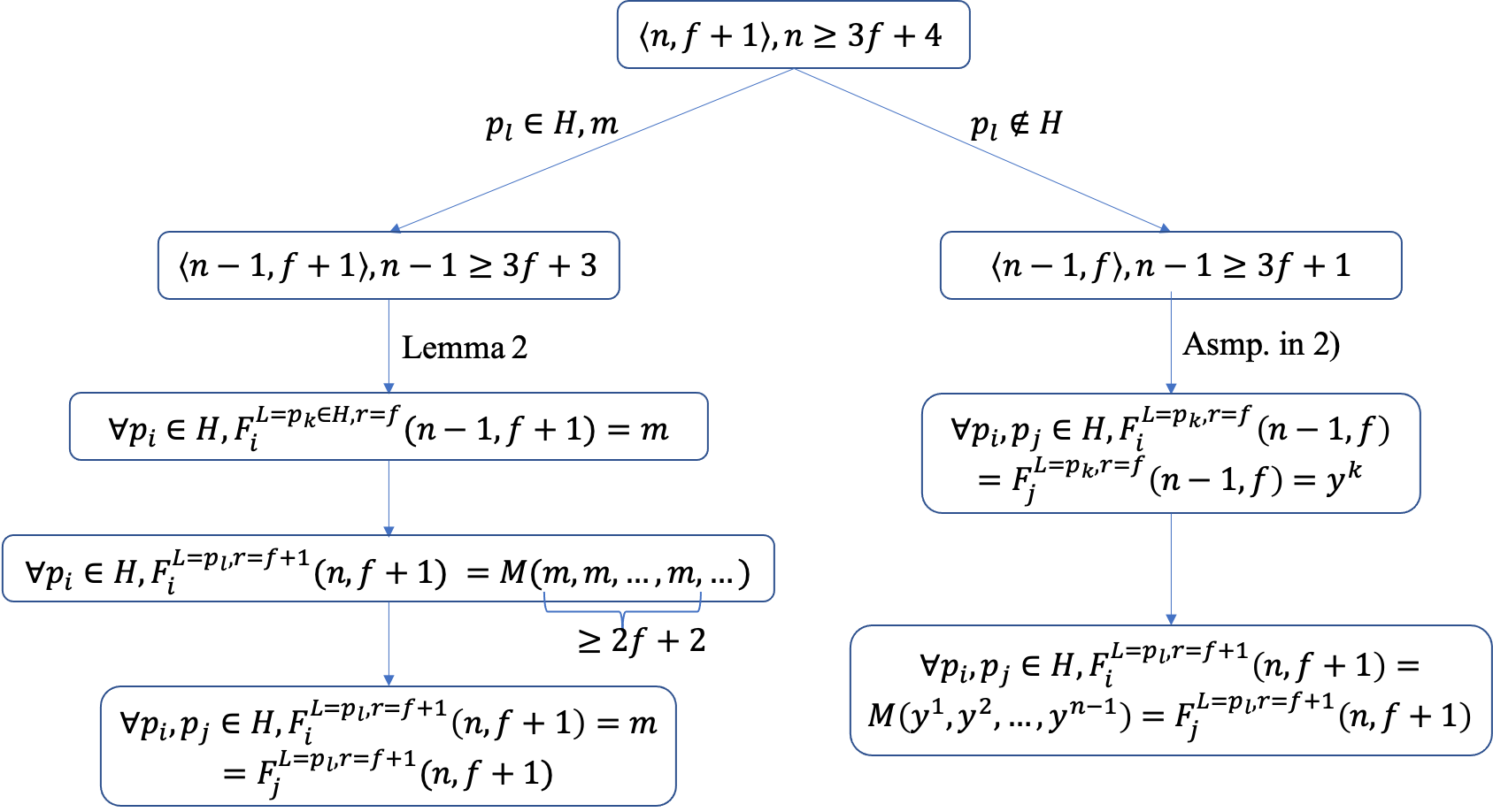
- Next, we consider the situation for \(f\)+1 and \(n \geq\) 3\(f\)+4.
- If the leader \(p_l\) is honest, the set {\(S|p_l\)} is consisted of \(n\)-1 replicas with \(f\)+1 Byzantine ones, where \(n\)-1 \(\geq\) 3(\(f\)+1). According to Lemma 2, we have \(F_i^{L\in H,r=f}(\)n\(-1, f+1)\) = \(F_j^{L\in H,r=f}(\)n\(-1, f+1)\). Therefore, back to the set \(S\) with \(p_l\) as the leader (broadcasting the message \(m\)), for a replica \(p_a\), \(\forall p_k \in H\), \(y_a^{k, r=f}\)=\(m\). The value set {\(y_a^{1, r=f}, y_a^{2, r=f}, ..., y_a^{n-1, r=f}\)} contains at least \(n\)-1-\(f\) values of \(m\). Thus, for any replica \(p_a\), \(F_a^{r=f+1}(n, f+1)\)=\(M_a(y_a^{1, r=f}, y_a^{2, r=f}, ..., y_a^{n-1, r=f})\)=\(m\).
- If the leader \(p_l\) is Byzantine, the set {\(S|p_l\)} is consisted of \(n\)-1 replicas with \(f\) Byzantine ones, where \(n\)-1 \(\geq\) 3\(f\)+3 \(\geq\) 3\(f\)+1. According to the assumption in 2), we have \(F_i^{r=f}(n-1, f)\) = \(F_j^{r=f}(n-1, f)\). Back to the set \(S\) with \(p_l\) as the leader, for a replica \(p_a\), the input argument \(y_a^{k,r=f}\)= \(F_a^{L=p_k,r=f}(n-1, f)\) for the function \(M_a\) will be always the same. Therefore \(F_a^{r=f+1}(n,f+1)\)=\(M_a(y_a^{1, r=f}, y_a^{2, r=f}, ..., y_a^{n-1, r=f})\) will be all the same too.
- To sum up, Theorem 1 is correct for \(f\)+1 and \(n \geq\) 3\(f\)+4.
- The proof path is demonstrated by Figure 3.