Seafooler's Blog
0%

Understanding the Responsiveness of Chained HotStuff

Posted on In

In the previous blog, we have talked about the safety of chained HotStuff.

In this post, we go on talking about its responsiveness.

I. Definition of responsiveness

The notion of responsiveness has been defined strictly in [1][2], such as follows:

After GST, any correct leader, once designated, needs to wait just for the first n − f responses to guarantee that it can create a proposal that will make progress. This includes the case where a leader is replaced.

However, this strict definition is obscure. Here, we give a unprecise description of responsiveness as follows:

The first block proposed by the new leader will be voted by each honest replica, if the block is received by the replica.

II. Why can three-phase commit promise the responsiveness?

First, let us talk about why three-phase commit can promise the responsiveness.

We do not want to explain the reason in a mathematical manner, which would be a little boring and hard for understanding. Instead, we will explain it through an example, which can be clearly compared with the example in Section III.

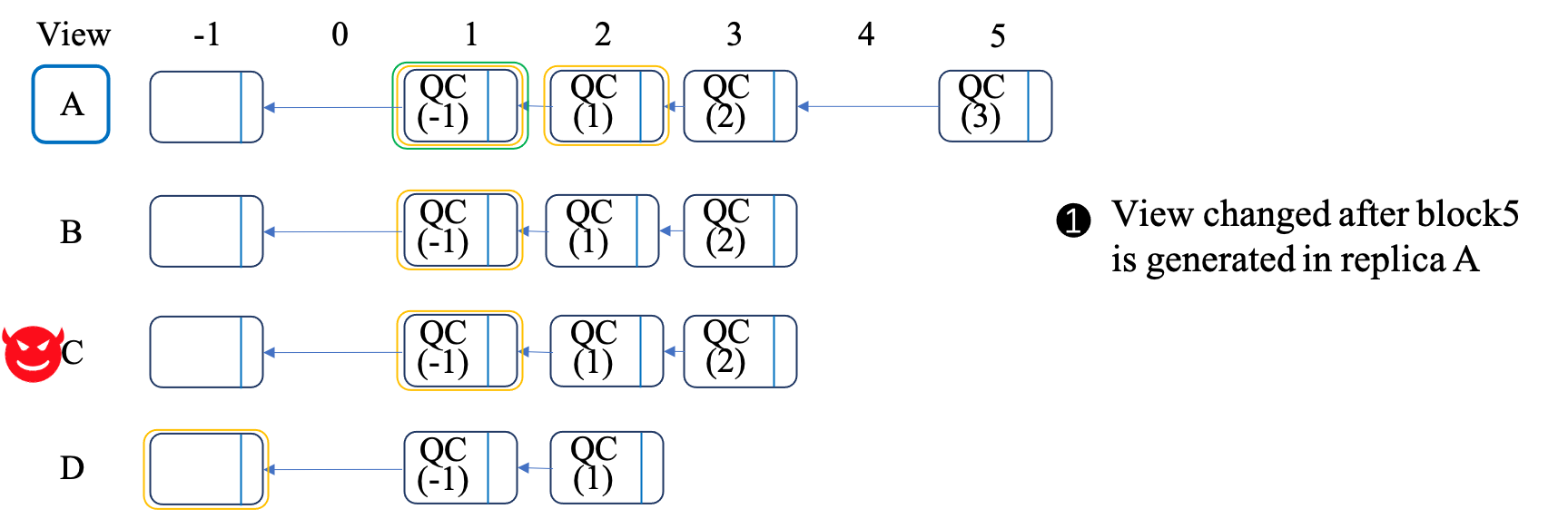
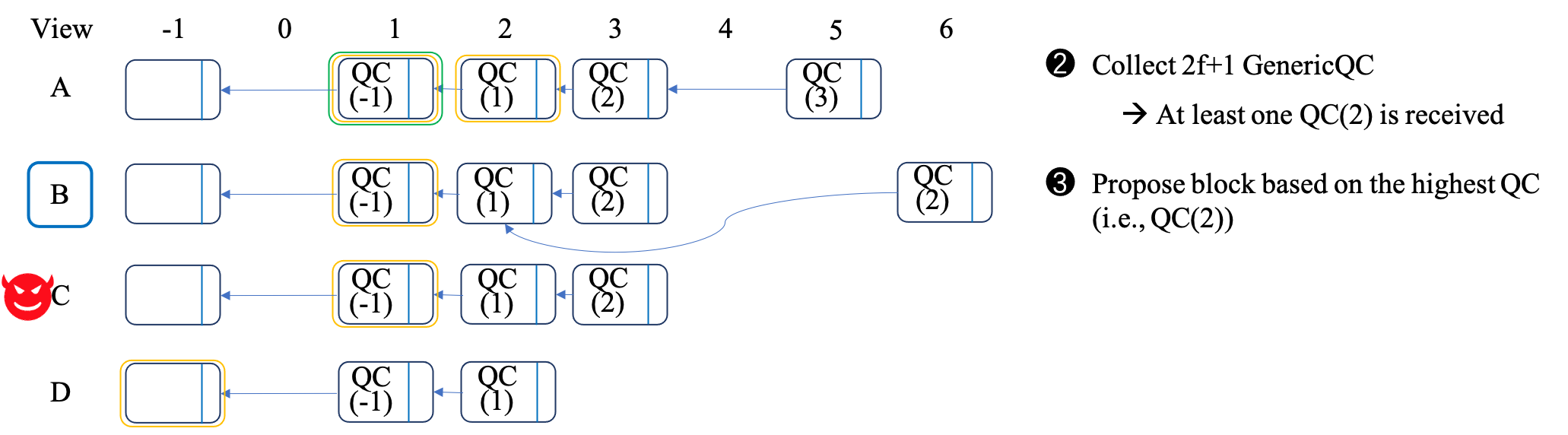
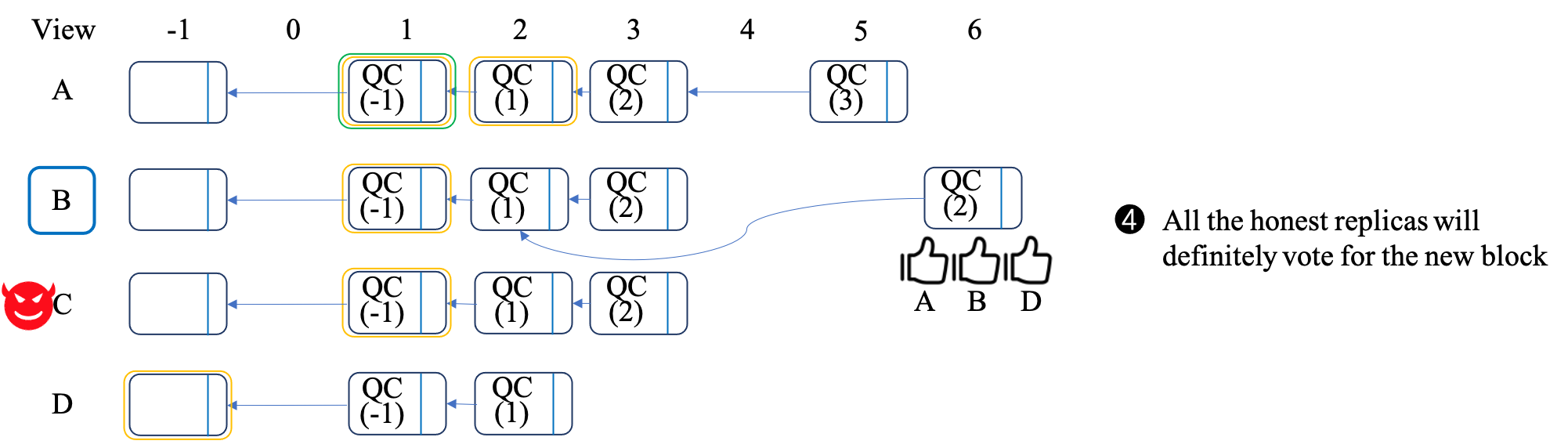
We present the example in four steps, corresonding to the three figures as follows: - As shown in Figure 1(a), the leader of the current view is replica A. After the block of height 5 (named as block5 for short) is generated in replica A, view is changed. At that time, block1 is committed and block2 is locked in replica A. On the other hand, since block5 contains a QC for block3, at least \(2f+1\) (i.e., 3) replicas have received and voted for block2. Therefore, at least \(2f+1\) (i.e., 3) replicas, for example replicas A, B and C, have locked block1. Besides, replicas A, B, and D will send the GenericQC of QC(3), QC(2), and QC(1) to the new leader, respectively. - As shown in Figure 1(b), the next leader is replica B, which will first collect \(2f+1\) GenericQC. According to the above analysis, it will receive at least one QC(2) or higher. Suppose the highest QC received by B is QC(2). Therefore, it will propose a new block based on QC(2), i.e., block6. - As shown in Figure 1(c), block6 is the descendent of the locked block in all the honest replicas (i.e., A, B, D). Therefore, all the honest replicas will vote for the new block, namely achieving the responsiveness.

Figure 1 (a). Before view change
Figure 1 (b). During view change
Figure 1 (c). After view change

III. Why cannot two-phase commit promise the responsiveness?

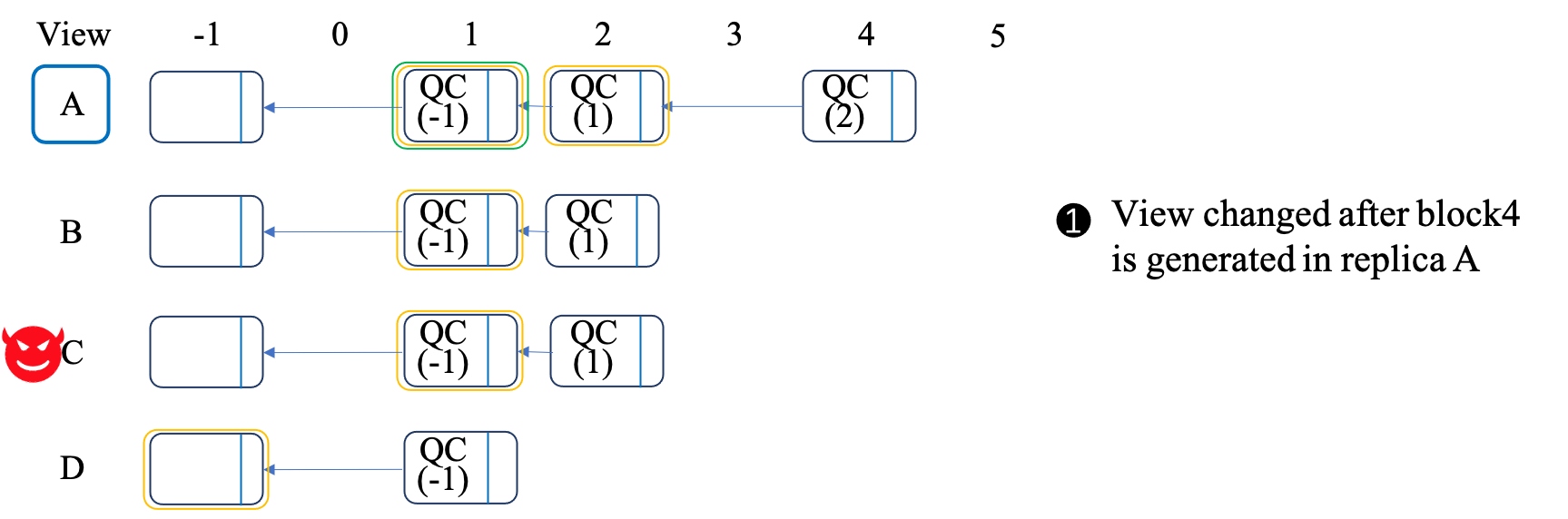
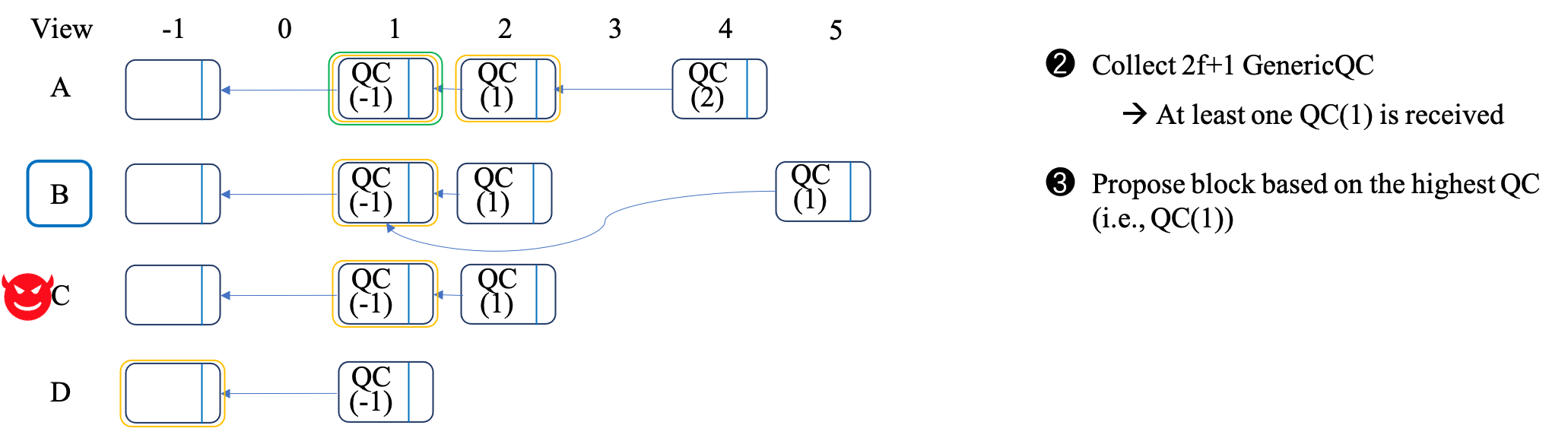
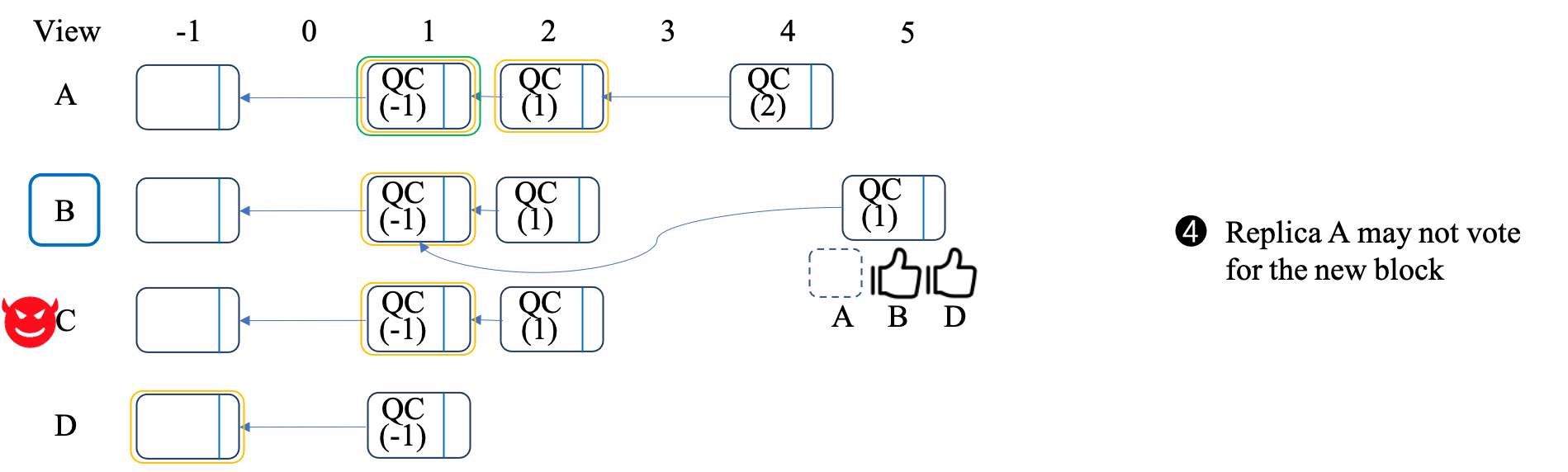
Our reason is also explained through an example, which is quite similar to Section II: - As shown by Figure 2(a), the view is changed after block4 is generated in replica A. At that time, replica A commits block1 and lock block2. Replicas B and C lock block1, while replica D locks block(-1). Besides, replica A, B, and D will send the GenericQC of QC(2), QC(1), and QC(-1) to the new leader, respectively. - As shown by Figure 2(b), the new leader is replica B, which will collect \(2f+1\) (i.e., 3) GenericQC. At least one QC(1) or higher will be received by B. Therefore, in the worst situation, the highest QC received by B is QC(1) and B will propose a new block based on QC(1), namely block5 in Figure 2(b). - As shown by Figure 2(c), since block5 is not the descendant of A's local chain and block5's QC (QC(1)) is not higher than A's locked block (QC(1)), it will not vote for block5. Thus, the two-phase commit cannot promise the responsiveness.

Figure 2 (a). Before view change
Figure 2 (b). During view change
Figure 2 (c). After view change

Reference

  1. Yin, M., Malkhi, D., Reiter, M. K., Gueta, G. G., & Abraham, I. "HotStuff: BFT consensus with linearity and responsiveness." In Proceedings of the 2019 ACM Symposium on Principles of Distributed Computing (PODC'19), pp. 347-356.
  2. Pass, R., Shi, E. "Thunderella: Blockchains with optimistic instant confirmation." In Proceedings of Annual International Conference on the Theory and Applications of Cryptographic Techniques (EuroCrypt'18), pp. 3-33.